题目内容
椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆C的方程;
(2)若M为右准线上一点,A为椭圆C的左顶点,连接AM交椭圆于点P,求
| PM |
| AP |
(3)圆x2+(y-t)2=1上任一点为D,曲线C上任一点为E,如果线段DE长的最大值为2
| 5 |
分析:(1)由题意得,c=2,
=8,由此能求出椭圆方程.
(2)设P点横坐标为x0,则
=
=
-1,由-4<x0≤4,知
=
=
-1≥
.由此能求出
的取值范围.
(3)设圆的圆心为O,因圆的半径为1,故OE的最大值为2
,设E(x0,y0),则
=16(1-
),OE=
=
,由-2
≤y0≤2
,能够推导出t=±1.
| a2 |
| c |
(2)设P点横坐标为x0,则
| PM |
| AP |
| 8-x0 |
| x0+4 |
| 12 |
| x0+4 |
| PM |
| AP |
| 8-x0 |
| x0+4 |
| 12 |
| x0+4 |
| 1 |
| 2 |
| PM |
| AP |
(3)设圆的圆心为O,因圆的半径为1,故OE的最大值为2
| 5 |
| x | 2 0 |
| y02 |
| 12 |
|
16-
|
| 3 |
| 3 |
解答:解:(1)由题意得,c=2,
=8得,a2=16,b2=12,
∴所求椭圆方程为
+
=1.…(5分)
(2)设P点横坐标为x0,则
=
=
-1,…(7分)
∵-4<x0≤4,∴
=
=
-1≥
.
∴
的取值范围是[
,+∞)…(10分)
(3)设圆的圆心为O,因圆的半径为1,因此,OE的最大值为2
,
设E(x0,y0),则
+
=1,即
=16(1-
)
则OE=
=
=
=
…(12分)
∵-2
≤y0≤2
∴当-2
≤-3t≤2
时,则y0=-3t时,有OEmax=
=2
,得t=±1,满足条件;…(14分)
当-3t>2
时,则y0=2
时,有OEmax=
=2
,得,t=2
±2
,但均不满足条件,所以无解;
当-3t<-2
时,同理可得无解.…(16分)
所以,t=±1.
| a2 |
| c |
∴所求椭圆方程为
| x2 |
| 16 |
| y2 |
| 12 |
(2)设P点横坐标为x0,则
| PM |
| AP |
| 8-x0 |
| x0+4 |
| 12 |
| x0+4 |
∵-4<x0≤4,∴
| PM |
| AP |
| 8-x0 |
| x0+4 |
| 12 |
| x0+4 |
| 1 |
| 2 |
∴
| PM |
| AP |
| 1 |
| 2 |
(3)设圆的圆心为O,因圆的半径为1,因此,OE的最大值为2
| 5 |
设E(x0,y0),则
| x02 |
| 16 |
| y02 |
| 12 |
| x | 2 0 |
| y02 |
| 12 |
则OE=
|
16-
|
-
|
-
|
∵-2
| 3 |
| 3 |
∴当-2
| 3 |
| 3 |
| 16+4t2 |
| 5 |
当-3t>2
| 3 |
| 3 |
-
|
| 5 |
| 3 |
| 5 |
当-3t<-2
| 3 |
所以,t=±1.
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
相关题目
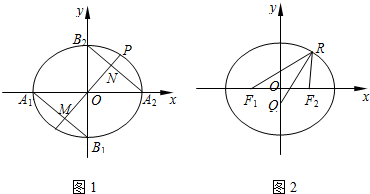
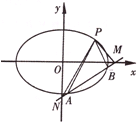 如图,已知椭圆C:
如图,已知椭圆C: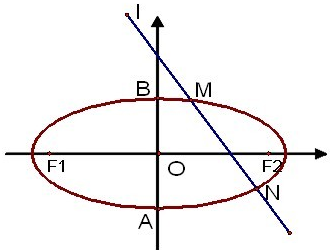 如图所示,椭圆C:
如图所示,椭圆C: