题目内容
一条斜率为1的直线l与离心率e=
的椭圆C:
+
=1(a>b>0)交于P、Q两点,直线l与y轴交于点R,且
•
=-3,
=3
,求直线l和椭圆C的方程.
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
. |
| OP |
. |
| OQ |
. |
| PR |
. |
| RQ |
分析:由e=
,知
=
,a2=2b2,则椭圆方程为
+
=1,设l方程为:y=x+m,P(x1,y1),Q(x2,y2),
联立
,得3x2+4mx+2m2-2b2=0,故有△=16m2-4×3(2m2-2b2)=8(-m2+3b2)>0.由此入手能求出直线l方程和椭圆C的方程.
| ||
| 2 |
| c |
| a |
| ||
| 2 |
| x2 |
| 2b2 |
| y2 |
| b2 |
联立
|
解答:解:∵e=
,∴
=
,a2=2b2,则椭圆方程为
+
=1,
设l方程为:y=x+m,P(x1,y1),Q(x2,y2),
联立
,去y得3x2+4mx+2m2-2b2=0,
故有△=16m2-4×3(2m2-2b2)=8(-m2+3b2)>0
∴3b2>m2(*)
x1+x2=-
m(1)
x1x2=
(m2-b2)(2)
又
•
=-3得x1x2+y1y2=-3,
而y1y2=(x1+m)(x2+m)=x1x2+m(x1+x2)+m2,
所以2x1x2+m(x1+x2)+m2=-3,
故
(m2-b2)-
m2+m2=-3,∴3m2-4b2=-9(3)
又R(0,m),
=3
,(-x1,m-y1)=3(x2,y2-m)
从而-x1=3x2(4)
由(1)(2)(4)得3m2=b2(5)
由(3)(5)解得b2=3,m=±1适合(*),
∴所求直线l方程为y=x+1或y=x-1;椭圆C的方程为
+
=1.
| ||
| 2 |
| c |
| a |
| ||
| 2 |
| x2 |
| 2b2 |
| y2 |
| b2 |
设l方程为:y=x+m,P(x1,y1),Q(x2,y2),
联立
|
故有△=16m2-4×3(2m2-2b2)=8(-m2+3b2)>0
∴3b2>m2(*)
x1+x2=-
| 4 |
| 3 |
x1x2=
| 2 |
| 3 |
又
| OP |
| OQ |
而y1y2=(x1+m)(x2+m)=x1x2+m(x1+x2)+m2,
所以2x1x2+m(x1+x2)+m2=-3,
故
| 4 |
| 3 |
| 4 |
| 3 |
又R(0,m),
| PR |
| RQ |
从而-x1=3x2(4)
由(1)(2)(4)得3m2=b2(5)
由(3)(5)解得b2=3,m=±1适合(*),
∴所求直线l方程为y=x+1或y=x-1;椭圆C的方程为
| x2 |
| 6 |
| y2 |
| 3 |
点评:本题考查直线和椭圆的位置关系的综合运用,综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的椭圆C:
的椭圆C: +
+ =1(a>b>0)交于P、Q两点,直线l与y轴交于点R,且
=1(a>b>0)交于P、Q两点,直线l与y轴交于点R,且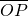 •
•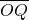 =-3,
=-3, =3
=3 ,求直线l和椭圆C的方程.
,求直线l和椭圆C的方程. 的双曲线
的双曲线 交于P、Q两点,直线l与y轴交于点R,且
交于P、Q两点,直线l与y轴交于点R,且 ,
,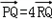 ,求直线与双曲线方程
,求直线与双曲线方程