题目内容
直角坐标系xoy中,已知椭圆C:
+
=1(a>b>0)的左、右顶点分别是A1,A2,上、下顶点为B2,B1,点P(
a,m)(m>0)是椭圆C上一点,PO⊥A2B2,直线PO分别交A1B1、A2B2于点M、N.
(1)求椭圆离心率;
(2)若MN=
,求椭圆C的方程;
(3)在(2)的条件下,设R点是椭圆C上位于第一象限内的点,F1、F2是椭圆C的左、右焦点,RQ平分∠F1RF2且与y轴交于点Q,求点Q纵坐标的取值范围.

| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 5 |
(1)求椭圆离心率;
(2)若MN=
4
| ||
| 7 |
(3)在(2)的条件下,设R点是椭圆C上位于第一象限内的点,F1、F2是椭圆C的左、右焦点,RQ平分∠F1RF2且与y轴交于点Q,求点Q纵坐标的取值范围.

分析:(1)根据点P在椭圆上可把P点坐标用a,b表示出来,由PO⊥A2B2,可得KA2B2•KOP=-1,由此可得a,b的关系式,连同a2=b2+c2可求得e值;
(2)由MN=
可得关于a,b的一方程,再根据(1)中离心率值即可求得a,b值,从而求得椭圆方程;
(3)设R(x0,y0),Q(0,t),由题意得cos∠F1RQ=cos∠F2RQ,利用向量夹角公式可表示成关于y0与t的式子,根据y0的范围即可求得t的范围;
(2)由MN=
4
| ||
| 7 |
(3)设R(x0,y0),Q(0,t),由题意得cos∠F1RQ=cos∠F2RQ,利用向量夹角公式可表示成关于y0与t的式子,根据y0的范围即可求得t的范围;
解答:解:(1)因为点P在椭圆上,所以在方程中令x=
a,得m=
b,故P(
,
),
∵PO⊥A2B2,∴KA2B2•KOP=-1,即-
×
=-1,
∴4b2=3a2=4(a2-c2),∴a2=4c2,∴e=
①,
故椭圆的离心率为
;
(2)MN=
=
,∴
=
②
联立①②解得,a2=4,b2=3,
∴椭圆C的方程为:
+
=1.
(3)由(2)可得F1(-1,0),F2(1,0),
设∠F1RQ=α,∠F2RQ=β,则cosα=cosβ,
∴
=
.
设R(x0,y0),Q(0,t),
则
=
化简得:t=-
y0,
∵0<y0<
,t∈(-
,0).
故点Q纵坐标的取值范围为:(-
,0).
| 3 |
| 5 |
| 4 |
| 5 |
| 3a |
| 5 |
| 4b |
| 5 |
∵PO⊥A2B2,∴KA2B2•KOP=-1,即-
| b |
| a |
| ||
|
∴4b2=3a2=4(a2-c2),∴a2=4c2,∴e=
| 1 |
| 2 |
故椭圆的离心率为
| 1 |
| 2 |
(2)MN=
4
| ||
| 7 |
| 2 | ||||||
|
| a2+b2 |
| a2b2 |
| 7 |
| 12 |
联立①②解得,a2=4,b2=3,
∴椭圆C的方程为:
| x2 |
| 4 |
| y2 |
| 3 |
(3)由(2)可得F1(-1,0),F2(1,0),
设∠F1RQ=α,∠F2RQ=β,则cosα=cosβ,
∴
| ||||
|
|
| ||||
|
|
设R(x0,y0),Q(0,t),
则
| (-1-x0,-y0)(-x0,t-y 0) | ||
|
| (1-x0,-y0)(-x0,t-y 0) | ||
|
化简得:t=-
| 1 |
| 3 |
∵0<y0<
| 3 |
| ||
| 3 |
故点Q纵坐标的取值范围为:(-
| ||
| 3 |
点评:本题考查直线与圆锥曲线的位置关系以及椭圆标准方程的求解,考查学生综合运用所学知识分析问题解决问题的能力,属难题.

练习册系列答案
相关题目
在平面直角坐标系xOy中,不等式组
表示图形的面积等于( )
|
| A、1 | B、2 | C、3 | D、4 |
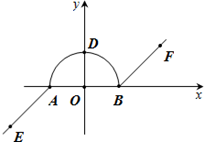 如图,在平面直角坐标系xOy中,我把由两条射线AE,BF和以AB为直径的半圆所组成的图形叫作图形C(注:不含AB线段).已知A(-1,0),B(1,0),AE∥BF,且半圆与y轴的交点D在射线AE的反向延长线上.
如图,在平面直角坐标系xOy中,我把由两条射线AE,BF和以AB为直径的半圆所组成的图形叫作图形C(注:不含AB线段).已知A(-1,0),B(1,0),AE∥BF,且半圆与y轴的交点D在射线AE的反向延长线上.