题目内容
(本小题满分12分)
已知f(x)=sin(2x+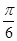 )+sin(2x-
)+sin(2x-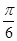 )+2cos2x+a,当x∈[-
)+2cos2x+a,当x∈[-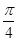 ,
,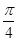 ]时,f(x)的最小值为-3,求α的值.
]时,f(x)的最小值为-3,求α的值.
已知f(x)=sin(2x+
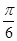 )+sin(2x-
)+sin(2x-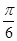 )+2cos2x+a,当x∈[-
)+2cos2x+a,当x∈[-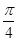 ,
,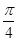 ]时,f(x)的最小值为-3,求α的值.
]时,f(x)的最小值为-3,求α的值.a=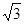 -4.
-4.
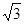 -4.
-4.本试题主要是考查了三角函数中两角和差的三角公式的运用,以及二倍角公式的综合运用。三角函数的性质的综合试题。首先化为单一函数,然后分析定义域和单调性,进而确定最值。
解:∵f(x)=sin(2x+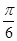 )+sin(2x-
)+sin(2x-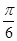 )+2cos2x+a
)+2cos2x+a
=3sin2x+cos2x+1+a=2sin(2x+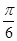 )+1+a.
)+1+a.
∵x∈[-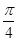 ,
,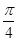 ],∴-
],∴-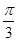 ≤2x+
≤2x+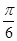 ≤
≤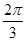 .
.
∴f(x)在[-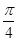 ,
,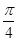 ]上的最小值为2(-
]上的最小值为2(-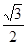 )+1+a=1-
)+1+a=1-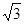 +a.
+a.
由题意,知1-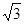 +a=-3,∴a=
+a=-3,∴a=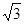 -4.
-4.
解:∵f(x)=sin(2x+
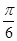 )+sin(2x-
)+sin(2x-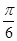 )+2cos2x+a
)+2cos2x+a=3sin2x+cos2x+1+a=2sin(2x+
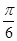 )+1+a.
)+1+a.∵x∈[-
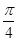 ,
,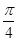 ],∴-
],∴-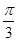 ≤2x+
≤2x+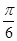 ≤
≤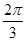 .
.∴f(x)在[-
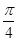 ,
,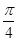 ]上的最小值为2(-
]上的最小值为2(-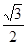 )+1+a=1-
)+1+a=1-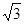 +a.
+a.由题意,知1-
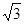 +a=-3,∴a=
+a=-3,∴a=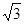 -4.
-4.
练习册系列答案
相关题目
 .
. 的最小正周期、最小值、最大值;
的最小正周期、最小值、最大值;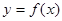 区间
区间 内的图象.
内的图象.
 的图象如图2所示,则
的图象如图2所示,则 。
。
 )的图象,应该把函数y=sin2x的图象( )
)的图象,应该把函数y=sin2x的图象( )
 cos2x+sinxcosx-
cos2x+sinxcosx- 的周期是( )
的周期是( )

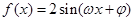 (
(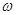 >0,0<
>0,0<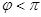 )的最小正周期为
)的最小正周期为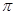 ,且
,且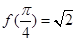 .
. 的值;
的值;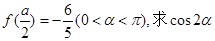
 4sin x
4sin x 的部分图像如右图所示,设
的部分图像如右图所示,设 是图像的一个最高点,
是图像的一个最高点, 是图像与
是图像与 轴的交点,若
轴的交点,若 ,则
,则

 ,
,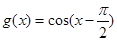 ,则下列命题中正确的是 ( )
,则下列命题中正确的是 ( ) 是偶函数
是偶函数 

