题目内容
已知函数y=anx2(an≠0,n∈N*)的图象在x=1处的切线斜率为2an-1+1(n≥2),且当n=1时其图象过点(2,8),则a7的值为________.
5
【解析】因为y=anx2在x=1处的切线斜率为2an,所以2an=2an-1+1(n≥2),即an=an-1+ (n≥2),又8=4a1⇒a1=2,所以a7=a1+6×
(n≥2),又8=4a1⇒a1=2,所以a7=a1+6×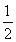 =5.
=5.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
题目内容
已知函数y=anx2(an≠0,n∈N*)的图象在x=1处的切线斜率为2an-1+1(n≥2),且当n=1时其图象过点(2,8),则a7的值为________.
5
【解析】因为y=anx2在x=1处的切线斜率为2an,所以2an=2an-1+1(n≥2),即an=an-1+ (n≥2),又8=4a1⇒a1=2,所以a7=a1+6×
(n≥2),又8=4a1⇒a1=2,所以a7=a1+6×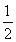 =5.
=5.

 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案