如图.在正三棱柱ABC-A1B1C1中.侧棱长为2$\sqrt{2}$.底面三角形的边长为2.则BC1与侧面ACC1A1所成角的大小为30°．题目和参考答案——青夏教育精英家教网——

题目内容

16．

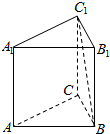如图，在正三棱柱ABC-A₁B₁C₁中，侧棱长为2$\sqrt{2}$，底面三角形的边长为2，则BC₁与侧面ACC₁A₁所成角的大小为30°．

分析取AC的中点E，连接BE，C₁E，∠BC₁E就是BC₁与侧面ACC₁A₁所成的角，由此能求出BC₁与侧面ACC₁A₁所成角的大小．

解答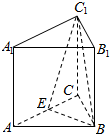解：取AC的中点E，连接BE，C₁E，
∵正三棱柱ABC-A₁B₁C₁中，∴BE⊥面ACC₁A₁，
∴∠BC₁E就是BC₁与侧面ACC₁A₁所成的角，
BC₁=$2\sqrt{3}$，BE=$\sqrt{4-1}$=$\sqrt{3}$，
∴sin∠BC₁E=$\frac{BE}{B{C}_{1}}$=$\frac{\sqrt{3}}{2\sqrt{3}}$=$\frac{1}{2}$，
∴∠BC₁E=30°．
∴BC₁与侧面ACC₁A₁所成角为30°．
故答案为：30°．

点评本题考查线面角的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．

练习册系列答案

黄冈经典阅读系列答案

文言文课外阅读特训系列答案

轻松阅读训练系列答案

南大教辅初中英语任务型阅读与首字母填空系列答案

初中英语听力与阅读系列答案

领航英语阅读理解与完形填空系列答案

英语拓展听力与阅读系列答案

阅读组合突破系列答案

初中英语阅读系列答案

全程探究阅读系列答案

相关题目

6．已知a，b，c，d≠0，c，d是x²+ax+b=0的解，a，b是x²+cx+d=0的解，求证：（a+b+c+d）²=abcd．

7．已知函数f（x）=（1+$\sqrt{3}$tanx）•cos²x，
（Ⅰ）当x∈[$\frac{π}{6}$，$\frac{π}{2}$）时，求函数f（x）的取值范围；
（Ⅱ）若在△ABC中，AC=2，BC=2$\sqrt{3}$，f（$\frac{A}{2}$）=$\frac{3}{2}$，求△ABC的面积．

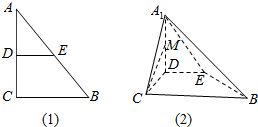如图（1），在Rt△ABC中，∠C=90°，BC=2，AC=4，点D，E分别是AC，AB的中点，将△ADE沿DE折起到△A₁DE的位置，使A₁D⊥DC如图（2）所示，M为A₁D的中点，求CM与面A₁EB所成角的正弦值．

11．若f（x）是定义在（0，+∞）上的增函数，且对一切x，y＞0，满足f（$\frac{x}{y}$）=f（x）-f（y），
（1）求f（1）的值；
（2）证明f（x²）=2f（x）（x＞0）；
（3）若f（4）=1，解关于x不等式f（x²+$\frac{8}{3}$x）-f（$\frac{1}{3}$）＜2．

1．若a=i+i²+…+i²⁰¹³（i是虚数单位），则$\frac{a（1+a）^{2}}{1-a}$的值为（　　）

8．下列命题中，判断条件p是条件q的什么条件：
（1）p：|x|=|y|，q：x=y；
（2）p：△ABC是直角三角形，q：△ABC是等腰三角形；
（3）p：四边形的对角线互相平分，q：四边形是矩形；
（4）p：p且q是真命题，q：非p为假命题．

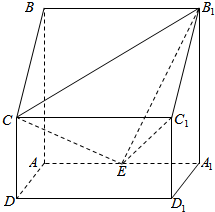四棱柱ABCD-A₁B₁C₁D₁中，侧棱AA₁⊥底面ABCD，AB∥CD，AB⊥AD，AD=CD=1，AA₁=AB=2，E为棱AA₁的中点．
（1）求证：B₁C₁⊥CE
（2）求点C到平面B₁C₁E的距离．

6．左、右焦点分别为F₁、F₂的椭圆C₁：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）与焦点为F的抛物线C₂：x²=2y相交于A、B两点，若四边形ABF₁F₂为矩形，且△ABF的周长为3+2$\sqrt{2}$．
（1）求椭圆C₁的方程；
（2）过椭圆C₁上一动点P（不在x轴上）作圆O：x²+y²=1的两条切线PC、PD，切点分别为C、D，直线CD与椭圆C₁交于E、G两点，O为坐标原点，求△OEG的面积S_△OEG的取值范围．