题目内容
11.若f(x)是定义在(0,+∞)上的增函数,且对一切x,y>0,满足f($\frac{x}{y}$)=f(x)-f(y),(1)求f(1)的值;
(2)证明f(x2)=2f(x)(x>0);
(3)若f(4)=1,解关于x不等式f(x2+$\frac{8}{3}$x)-f($\frac{1}{3}$)<2.
分析 (1)令x=y=1,即可求得f(1)的值;
(2)令y=$\frac{1}{x}$,得到f(x2)=f(x)-f($\frac{1}{x}$),而f($\frac{1}{x}$)=f(1)-f(x)=-f(x),问题得以证明.
(3)令x=16,y=4,求出f(16)=2,根据函数的单调性得到不等式组,解得即可.
解答 解:(1)令x=y=1,由f($\frac{x}{y}$)=f(x)-f(y),
可得f(1)=f(1)-f(1),
即有f(1)=0;
(2)令y=$\frac{1}{x}$,
∴f(x2)=f(x)-f($\frac{1}{x}$)=f(x)-[f(1)-f(x)]=f(x)+f(x)=2f(x),
∴f(x2)=2f(x)(x>0);
(3)令x=16,y=4,
∴f(4)=f(16)-f(4),
∴f(16)=2f(4)=2,
∵f(x2+$\frac{8}{3}$x)-f($\frac{1}{3}$)<2,
∴f(3x2+8x)<f(16),
∵f(x)是定义在(0,+∞)上的增函数,
∴$\left\{\begin{array}{l}{3{x}^{2}+8x>0}\\{3{x}^{2}+8x<16}\end{array}\right.$,
解得:-4<x<-$\frac{8}{3}$,或0<x<$\frac{4}{3}$,
∴不等式得解集(-4,-$\frac{8}{3}$)∪(0,$\frac{4}{3}$).
点评 本题主要考查抽象函数的应用,利用赋值法是解决抽象函数的基本方法.结合函数的单调性是解决本题的关键.

练习册系列答案
相关题目
2.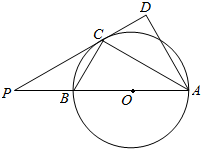 如图,AB是⊙O的直径,点C是⊙O上一点,AD⊥DC于D,且AC平分∠DAB,延长DC交AB的延长线于点P.
如图,AB是⊙O的直径,点C是⊙O上一点,AD⊥DC于D,且AC平分∠DAB,延长DC交AB的延长线于点P.
(1)求证:PC2=PA•PB;
(2)若3AC=4BC,⊙O的直径为7,求线段PC的长.
 如图,AB是⊙O的直径,点C是⊙O上一点,AD⊥DC于D,且AC平分∠DAB,延长DC交AB的延长线于点P.
如图,AB是⊙O的直径,点C是⊙O上一点,AD⊥DC于D,且AC平分∠DAB,延长DC交AB的延长线于点P.(1)求证:PC2=PA•PB;
(2)若3AC=4BC,⊙O的直径为7,求线段PC的长.
6.设集合A={x|0<x<4},B={x|x<a}若A⊆B,则实数a的取值范围是( )
| A. | {a|a≤0} | B. | {a|0<a≤4} | C. | {a|a≥4} | D. | {a|0<a<4} |
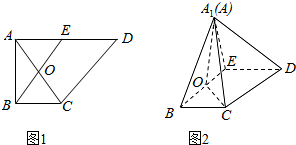 如图1,在直角梯形ABCD中,AD∥BC,AD⊥AB,AB=BC=$\frac{1}{2}$AD,E是AD的中点,O是AC与BE的交点,将△ABE沿BE折起到△A1BE的位置,如图2,
如图1,在直角梯形ABCD中,AD∥BC,AD⊥AB,AB=BC=$\frac{1}{2}$AD,E是AD的中点,O是AC与BE的交点,将△ABE沿BE折起到△A1BE的位置,如图2,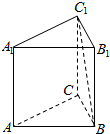 如图,在正三棱柱ABC-A1B1C1中,侧棱长为2$\sqrt{2}$,底面三角形的边长为2,则BC1与侧面ACC1A1所成角的大小为30°.
如图,在正三棱柱ABC-A1B1C1中,侧棱长为2$\sqrt{2}$,底面三角形的边长为2,则BC1与侧面ACC1A1所成角的大小为30°.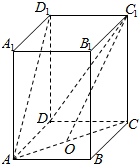 如图,在长方体中ABCD-A1B1C1D1,AB=3,BC=AA1=4,点O是AC的中点.
如图,在长方体中ABCD-A1B1C1D1,AB=3,BC=AA1=4,点O是AC的中点.