题目内容
【题目】已知函数![]() .
.
(1)求函数![]() 的单调递增区间;
的单调递增区间;
(2)在![]() 中,内角A,B,C所对的边分别为a,b,c,若
中,内角A,B,C所对的边分别为a,b,c,若![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用三角函数恒等变换的应用化简函数解析式可得f(x)=2sin(2x![]() ),利用正弦函数的单调性即可求解其单调递增区间.
),利用正弦函数的单调性即可求解其单调递增区间.
(2)由题意可得sin(2A![]() )=1,结合范围2A
)=1,结合范围2A![]() ∈(
∈(![]() ,
,![]() ),可求A的值,由正弦定理可得a,由余弦定理b,进而根据三角形的面积公式即可求解.
),可求A的值,由正弦定理可得a,由余弦定理b,进而根据三角形的面积公式即可求解.
(1)∵![]() sin2x﹣cos2x=2sin(2x
sin2x﹣cos2x=2sin(2x![]() ),
),
令2kπ![]() 2x
2x![]() 2kπ
2kπ![]() ,k∈Z,解得kπ
,k∈Z,解得kπ![]() x≤kπ
x≤kπ![]() ,k∈Z,
,k∈Z,
∴函数f(x)的单调递增区间为:[kπ![]() ,kπ
,kπ![]() ],k∈Z.
],k∈Z.
(2)∵f(A)=2sin(2A![]() )=2,
)=2,
∴sin(2A![]() )=1,
)=1,
∵A∈(0,π),2A![]() ∈(
∈(![]() ,
,![]() ),
),
∴2A![]() ,解得A
,解得A![]() ,
,
∵C![]() ,c=2,
,c=2,
∴由正弦定理![]() ,可得a
,可得a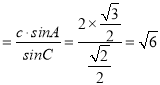 ,
,
∴由余弦定理a2=b2+c2﹣2bccosA,可得6=b2+4﹣2![]() ,解得b=1
,解得b=1![]() ,(负值舍去),
,(负值舍去),
∴S△ABC![]() absinC
absinC![]() (1
(1![]() )
)![]() .
.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目