题目内容
18.${log_2}\frac{2}{3}+{log_2}\frac{3}{2}+{(\frac{8}{27})^{-\frac{1}{3}}}$=$\frac{3}{2}$.分析 直接由对数的运算性质化简得答案.
解答 解:$lo{g}_{2}\frac{2}{3}+lo{g}_{2}\frac{3}{2}+(\frac{8}{27})^{-\frac{1}{3}}$=$lo{g}_{2}1+[(\frac{2}{3})^{3}]^{-\frac{1}{3}}$=$lo{g}_{2}1+\frac{3}{2}$=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 本题考查了对数的运算性质,是基础题.

练习册系列答案
相关题目
6.设a=log36,b=2-2,c=log${\;}_{\frac{1}{2}}$2,则( )
| A. | a>b>c | B. | b>c>a | C. | c>b>a | D. | c>a>b |
10.设a,b是实数,命题“?ab>0,都有a>0,b>0”的否定是( )
| A. | ?ab≤0,使得a≤0,b≤0 | B. | ?ab≤0,使得a≤0或b≤0 | ||
| C. | ?ab>0,使得a≤0,b≤0 | D. | ?ab>0,使得a≤0或b≤0 |
7.下列函数中值域为(0,+∞)的是( )
| A. | $y={2}^{{x}^{2}+1}$ | B. | y=$\frac{x+2}{x-1}$ | C. | y=$\sqrt{1-{2}^{x}}$ | D. | y=$(\frac{1}{3})^{1-x}$ |
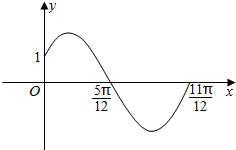 函数f(x)=Asin(ωx+ϕ)$(A>0,ω>0,0<ϕ<\frac{π}{2})$的部分图象如图所示.
函数f(x)=Asin(ωx+ϕ)$(A>0,ω>0,0<ϕ<\frac{π}{2})$的部分图象如图所示.