题目内容
有标号为1，2，3，4，5的五个红球和标号为1，2的两个白球，将这七个球排成一排，使两端都是红球.
①如果每个白球两边都是红球，共有多少种不同的排法？
②如果1号红球和1号白球相邻排在一起，共有多少种不同的排法？
③同时满足条件①②的排法有多少种？
【答案】
①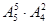
=1440（种）
②2
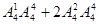=768（种）
③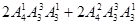
=576（种）
【解析】(1)按照先特殊再一般的原则进行排列即可.
（2）采用捆绑法把1号红球和1号白球当作一个元素要注意它本身的顺序.
（3）结合（1）（2）的做法进行排列即可
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目