题目内容
（2010•天津模拟）设O为坐标原点，点P的坐标（x-2，x-y）
（I）在一个盒子中，放有标号为1，2，3的三张卡片，现从此盒中有放回地先后抽到两张卡片的标号分别记为x，y，求|OP|的最大值，并求事件“|OP|取到最大值”的概率；
（II）若利用计算机随机在[0，3]上先后取两个数分别记为x，y，求P点在第一象限的概率．
（I）在一个盒子中，放有标号为1，2，3的三张卡片，现从此盒中有放回地先后抽到两张卡片的标号分别记为x，y，求|OP|的最大值，并求事件“|OP|取到最大值”的概率；
（II）若利用计算机随机在[0，3]上先后取两个数分别记为x，y，求P点在第一象限的概率．
分析：（1）记先后抽到的两张卡片的标号为（x，y），列出所有情形，然后分别求出|OP|的值，从而得到最大值；
（2）求出点P落在第一象限所构成区域的面积，然后求出基本事件空间所表示的区域的面积，计算出二者的比值即可．
（2）求出点P落在第一象限所构成区域的面积，然后求出基本事件空间所表示的区域的面积，计算出二者的比值即可．
解答：解：（I）记抽到的卡片标号为（x，y），所有的情况分别为，
共9种．由表格可知|OP|的最大值为
…（5分）
设事件A为“|OP|取到最大值”，则满足事件A的（x，y）有（1，3），（3，1）两种情况，
∴P(A)=
…（7分）
（II）设事件B为“P点在第一象限”
若
，则其所表示的区域面积为3×3=9
由题意可得事件B满足
，
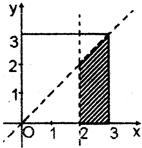
即如图所示的阴影部分，
其区域面积为1×3-
×1×1=
∴P(B)=
=
…（12分）
| （x，y） | （1，1） | （1，2） | （1，3） | （2，1） | （2，2） | （2，3） | （3，1） | （3，2） | （3，3） | ||||||||
| P（x-2，x-y） | （-1，0） | （-1，-1） | （-1，-2） | （0，1） | （0，0） | （0，-1） | （1，2） | （1，1） | （1，0） | ||||||||
| |OP| | 1 |
|
|
1 | 0 | 1 |
|
|
1 |
共9种．由表格可知|OP|的最大值为| 5 |
设事件A为“|OP|取到最大值”，则满足事件A的（x，y）有（1，3），（3，1）两种情况，
∴P(A)=
| 2 |
| 9 |
（II）设事件B为“P点在第一象限”
若
|
由题意可得事件B满足
|
即如图所示的阴影部分，
其区域面积为1×3-
| 1 |
| 2 |
| 5 |
| 2 |
∴P(B)=
| ||
| 9 |
| 5 |
| 18 |
点评：本题考查几何概率的求法：首先根据题意将代数关系用面积表示出来，一般用阴影区域表示所求事件（A）；然后计算阴影区域的面积在总面积中占的比例，这个比例即事件（A）发生的概率．
练习册系列答案
阅读快车系列答案
相关题目
（2010•天津模拟）某几何体的三视图，其中正视图是腰长为2的等腰三角形，侧视图是半径为1的半圆，则该几何体的表面积是