Question

【题目】给出下列说法，正确的有__________.

①与共线单位向量的坐标是；

②集合与集合是相等集合；

③函数的图象与的图象恰有3个公共点；

④函数的图象是由函数的图象水平向右平移一个单位后，将所得图象在轴右侧部分沿轴翻折到轴左侧替代轴左侧部分图象，并保留右侧部分而得到.

Answer 1

【答案】②④

【解析】

与（﹣3，4）共线的单位向量有两个，判定命题①是错误的；

分析出A、B两个集合均表示奇数集，可判断②；

分别画出函数的图象与y＝|x2﹣1|的图象，即可判断③；

运用函数图象平移变换和对称变换，即可判断④．

对于①，与（﹣3，4）共线的单位向量是（，）和（，），

∴命题①错误；

②集合与集合均表示奇数集，是相等集合，故②正确；

③分别画出函数的图象与y＝|x2﹣1|的图象，

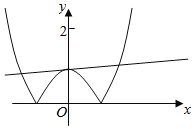
可得x＞1和x＜﹣1时，各有一个交点；

当﹣1＜x＜1时，y＝1﹣x2和y＝1+0.1x，联立可得x2+0.1x＝0，

即x＝0或x＝﹣0.1，则有两个交点；

函数的图象与y＝|x2﹣1|的图象共有4个公共点，故③错误；

④函数f（|x|﹣1）的图象是由函数f（x）的图象水平向右平移一个单位得到f（x-1）后，

再将所得图象在y轴右侧部分沿y轴翻折到y轴左侧替代y轴左侧部分图象，

并保留右侧部分而得到，故④正确；

综上可得①③错误；②④正确．

故答案为：②④．