题目内容
设不等式 的解集为M,
的解集为M,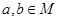 .
.
(1)证明: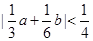 ;
;
(2)比较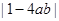 与
与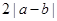 的大小,并说明理由.
的大小,并说明理由.
(1)证明过程详见解析;(2)|1-4ab|>2|a-b|.
解析试题分析:本题主要考查绝对值不等式的解法、绝对值的运算性质、作差法比较大小等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,先利用零点分段法将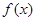 化为分段函数,解不等式求出M,再利用绝对值的运算性质化简得
化为分段函数,解不等式求出M,再利用绝对值的运算性质化简得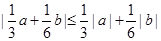 ,由于
,由于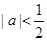 ,
,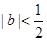 代入得
代入得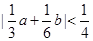 ;第二问,利用第一问的结论
;第二问,利用第一问的结论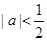 ,
,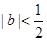 作差比较大小,由于
作差比较大小,由于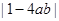 和
和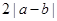 均为正数,所以都平方,作差比较大小.
均为正数,所以都平方,作差比较大小.
(1)记f(x)=|x-1|-|x+2|=
由-2<-2x-1<0解得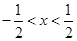 ,则
,则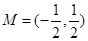 . 3分
. 3分
所以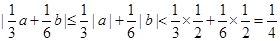 . 6分
. 6分
(2)由(1)得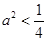 ,
,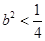 .
.
因为|1-4ab|2-4|a-b|2=(1-8ab+16a2b2)-4(a2-2ab+b2)
=(4a2-1)(4b2-1)>0, 9分
所以|1-4ab|2>4|a-b|2,故|1-4ab|>2|a-b|. 10分
考点:绝对值不等式的解法、绝对值的运算性质、作差法比较大小.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
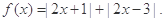
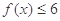 的解集;
的解集;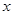 的不等式
的不等式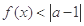 的解集非空,求实数
的解集非空,求实数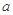 的取值范围.
的取值范围.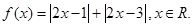 .
.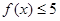 ;
;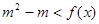 ,
, 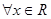 都成立,求实数
都成立,求实数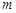 的取值范围.
的取值范围.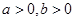 ,且
,且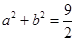 ,若
,若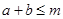 恒成立.
恒成立.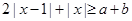 对任意的
对任意的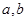 恒成立,求实数x的取值范围.
恒成立,求实数x的取值范围.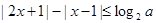 (其中
(其中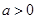 ).
).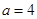 时,求不等式的解集;
时,求不等式的解集;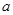 的取值范围
的取值范围 时,求不等式f(x)>1的解集.
时,求不等式f(x)>1的解集.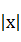 <1,
<1,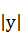 <1,求证:
<1,求证: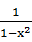 +
+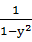 ≥
≥ .
.