题目内容
已知x,y∈R,且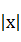 <1,
<1,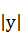 <1,求证:
<1,求证: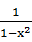 +
+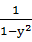 ≥
≥ .
.
见解析
解析证明:因为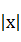 <1,
<1,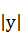 <1,所以
<1,所以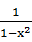 >0,
>0,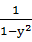 >0.
>0.
所以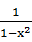 +
+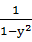 ≥
≥ .
.
故要证明结论成立,只需证 ≥
≥ 成立,
成立,
即证1-xy≥ 成立即可,
成立即可,
因为(y-x)2≥0,有-2xy≥-x2-y2,
所以(1-xy)2≥(1-x2)(1-y2),
所以1-xy≥ >0,
>0,
所以不等式成立.

练习册系列答案
相关题目
题目内容
已知x,y∈R,且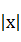 <1,
<1,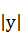 <1,求证:
<1,求证: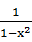 +
+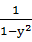 ≥
≥ .
.
见解析
解析证明:因为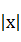 <1,
<1,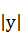 <1,所以
<1,所以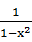 >0,
>0,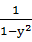 >0.
>0.
所以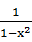 +
+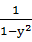 ≥
≥ .
.
故要证明结论成立,只需证 ≥
≥ 成立,
成立,
即证1-xy≥ 成立即可,
成立即可,
因为(y-x)2≥0,有-2xy≥-x2-y2,
所以(1-xy)2≥(1-x2)(1-y2),
所以1-xy≥ >0,
>0,
所以不等式成立.
