题目内容
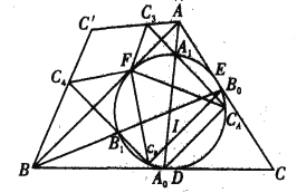
【题目】如图,![]() 的内切圆
的内切圆![]() 与三边BC、CA、AB分别切于点D、E、F,直线AI、BI与
与三边BC、CA、AB分别切于点D、E、F,直线AI、BI与![]() 分别交于点
分别交于点![]() .过点
.过点![]() 作边AB的平行线分别与
作边AB的平行线分别与![]() 交于点
交于点![]() ,联结
,联结![]() ,过点F作
,过点F作![]() 的一条垂线与
的一条垂线与![]() 交于点
交于点![]() ,过点F作
,过点F作![]() 的一条垂线与
的一条垂线与![]() 交于点
交于点![]() .设直线
.设直线![]() 与直线
与直线![]() 交于点C’,类似地,得到点A’、B’.证明:
交于点C’,类似地,得到点A’、B’.证明:![]() 的外接圆半径是
的外接圆半径是![]() 半径的2倍.
半径的2倍.
【答案】见解析
【解析】
先证明一个引理.
引理 如图,过![]() 外一点A作
外一点A作![]() 的一条切线AT,T为切点,再过A作一条直线与
的一条切线AT,T为切点,再过A作一条直线与![]() 交于B、C两点(AB<AC),过点C作AT的平行线与
交于B、C两点(AB<AC),过点C作AT的平行线与![]() 交于点D,过T作DT的一条垂线与DB交于点E.则∠BAT=∠EAT.
交于点D,过T作DT的一条垂线与DB交于点E.则∠BAT=∠EAT.
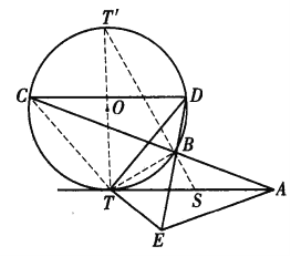
证明 设TO与![]() 的另一个交点为T’,联结T’B并延长,与AT交于点S,联结TB、TC.
的另一个交点为T’,联结T’B并延长,与AT交于点S,联结TB、TC.
则∠ABS=∠T’BC=∠DBT’=∠DTT’=90°-∠DTA=∠ATE.
又∠TDE=∠TDB=∠TT’B=∠BTS,∠DTE=∠TBS=90°.
故![]() .
.
又![]()
因此,![]() .
.
又∠ABS=∠DBT’=∠ATE,则![]()
![]() .
.
回到原题.
由引理知![]() ,
,![]()
![]() ,
,![]() .
.
![]() 为
为![]() 的中垂线.
的中垂线.
由![]()
![]() I’、F、C’三点共线,且F为C’I的中点
I’、F、C’三点共线,且F为C’I的中点
![]() (r为
(r为![]() 半径).
半径).
类似地,IA’=2r,IB’=2r.
故I为![]() 的外心,且
的外心,且![]() 的外接圆半径为
的外接圆半径为![]() 半径的2倍.
半径的2倍.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
【题目】每个国家对退休年龄都有不一样的规定,从2018年开始,我国关于延迟退休的话题一直在网上热议,为了了解市民对“延迟退休”的态度,现从某地市民中随机选取100人进行调查,调查情况如下表:
年龄段(单位:岁) |
|
|
|
|
|
|
被调查的人数 |
|
|
|
|
|
|
赞成的人数 |
|
|
|
|
|
|
(1)从赞成“延迟退休”的人中任选1人,此人年龄在![]() 的概率为
的概率为![]() ,求出表格中
,求出表格中![]() 的值;
的值;
(2)若从年龄在![]() 的参与调查的市民中按照是否赞成“延迟退休”进行分层抽样,从中抽取10人参与某项调查,然后再从这10人中随机抽取4人参加座谈会,记这4人中赞成“延迟退休”的人数为
的参与调查的市民中按照是否赞成“延迟退休”进行分层抽样,从中抽取10人参与某项调查,然后再从这10人中随机抽取4人参加座谈会,记这4人中赞成“延迟退休”的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.


