题目内容
设有编号为1,2,3,4,5的五个球和编号为1,2,3,4,5的五个盒子,现将这五个球放入5个盒子内. (答题要求:先列式,后计算)
(1)恰有一个盒子空着,共有多少种投放方法?
(2)每个盒子内投放一球,并且至少有两个球的编号与盒子编号是相同的,有多少种投放方法?
(1)恰有一个盒子空着,共有多少种投放方法?
(2)每个盒子内投放一球,并且至少有两个球的编号与盒子编号是相同的,有多少种投放方法?
见解析.
第一问中利用首先选定两个不同的球,看作一个球,选法有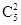 =10种,
=10种,
再把“空”当作一个球,共计5个“球”,投入5个盒子中即可
第二问中:不满足条件的情形:第一类,恰有一球相同的放法:
第二类,五个球的编号与盒子编号全不同的放法,分类讨论得到结论。
解:(1)首先选定两个不同的球,看作一个球,选法有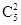 =10种,
=10种,
再把“空”当作一个球,共计5个“球”,投入5个盒子中,有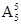 =120种投放法.∴共计10×120=1200种方法即
=120种投放法.∴共计10×120=1200种方法即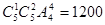
(2)不满足条件的情形:第一类,恰有一球相同的放法: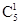 ×9=45,
×9=45,
第二类,五个球的编号与盒子编号全不同的放法:5!(1/ 2! -1/ 3! +1 /4! -1 /5! )=44
∴满足条件的放法数为:
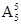 -45-44=31(种;………4分
-45-44=31(种;………4分
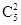 =10种,
=10种,再把“空”当作一个球,共计5个“球”,投入5个盒子中即可
第二问中:不满足条件的情形:第一类,恰有一球相同的放法:
第二类,五个球的编号与盒子编号全不同的放法,分类讨论得到结论。
解:(1)首先选定两个不同的球,看作一个球,选法有
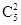 =10种,
=10种,再把“空”当作一个球,共计5个“球”,投入5个盒子中,有
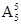 =120种投放法.∴共计10×120=1200种方法即
=120种投放法.∴共计10×120=1200种方法即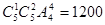
(2)不满足条件的情形:第一类,恰有一球相同的放法:
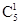 ×9=45,
×9=45,第二类,五个球的编号与盒子编号全不同的放法:5!(1/ 2! -1/ 3! +1 /4! -1 /5! )=44
∴满足条件的放法数为:
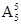 -45-44=31(种;………4分
-45-44=31(种;………4分
练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
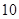 名队员中挑选
名队员中挑选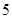 名上场比赛,要求甲、乙中至少有
名上场比赛,要求甲、乙中至少有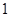 人参加,则下列选派方法种数表示不正确的是( ▲ )
人参加,则下列选派方法种数表示不正确的是( ▲ )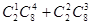
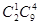
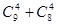
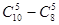
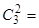 ______
______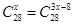 的解集为( )
的解集为( )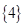
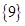
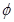
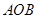 的边
的边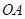 上有
上有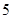 个点,边
个点,边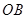 上有
上有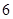 个点,加上
个点,加上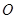 点共12个点,以这
点共12个点,以这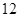 个点为顶点的三角形有 个.
个点为顶点的三角形有 个.