题目内容
已知三棱柱 的侧棱长和底面边长均为2,
的侧棱长和底面边长均为2, 在底面ABC内的射影O为底面△ABC的中心,如图所示:
在底面ABC内的射影O为底面△ABC的中心,如图所示:
(1)联结 ,求异面直线
,求异面直线 与
与 所成角的大小;
所成角的大小;
(2)联结 、
、 ,求四棱锥
,求四棱锥 的体积.
的体积.
(1) ;(2)
;(2)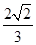 .
.
解析试题分析:(1)要求异面直线所成的角,必须按照定义作出这个角,即把异面直线平移为相交直线,求相交直线所夹的锐角或直角,当然我们一般是过异面直线中的某一条上一点作另一条直线的平行线,同时要借助已知图形中的平行关系寻找平行线,以方便解题.本题是三棱柱,显然有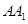 ∥
∥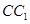 ,因此只要在
,因此只要在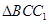 中求
中求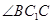 即可;(2)求四棱锥的体积,一般用公式
即可;(2)求四棱锥的体积,一般用公式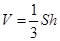 ,即底面面积乘以高再除以3,但本题中由于四棱锥的高不容易找,而这个棱锥在三棱柱中,因此我们可借助三棱柱来求棱锥的体积,利用棱锥体积的公式,可知三棱锥
,即底面面积乘以高再除以3,但本题中由于四棱锥的高不容易找,而这个棱锥在三棱柱中,因此我们可借助三棱柱来求棱锥的体积,利用棱锥体积的公式,可知三棱锥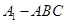 的体积是三棱柱体积的三分之一,因此所求四棱锥的体积正好是三棱柱的体积的三分之二,我们求出三棱柱的即可.
的体积是三棱柱体积的三分之一,因此所求四棱锥的体积正好是三棱柱的体积的三分之二,我们求出三棱柱的即可.
试题解析:(1) 联结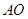 ,并延长与
,并延长与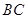 交于点
交于点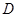 ,则
,则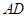 是
是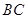 边上的中线.
边上的中线. 点
点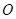 是正
是正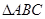 的中心,且
的中心,且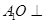 平面
平面 ,
,
∴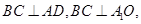 且
且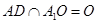 .∴
.∴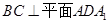 .
.
∴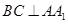 .
.
又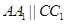 ,
,
∴异面直线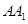 与
与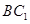 所成的角为
所成的角为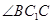 .
.
∴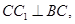 即四边形
即四边形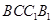 为正方形.
为正方形.
∴异面直线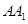 与
与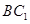 所成角的大小为
所成角的大小为 .
.
(2)∵三棱柱的所有棱长都为2,
∴可求算得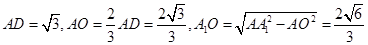 .
.
∴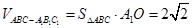 ,
,
∴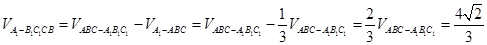 .
.
考点:(1)异面直线所成的角;(2)切割法与棱锥的体积.

练习册系列答案
相关题目
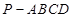 中,
中,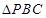 为正三角形,
为正三角形,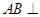 平面
平面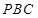 ,
,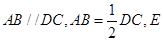 为
为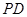 的中点.
的中点.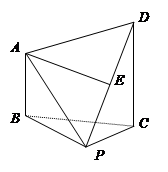
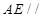 平面
平面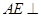 平面
平面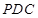 .
. 是正方形,
是正方形, 平面
平面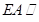
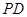 ,
,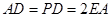 ,
,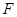 ,
,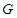 ,
, 分别为
分别为 ,
,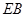 ,
, 的中点.
的中点.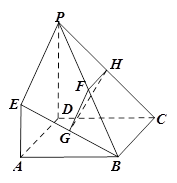
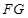
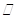 平面
平面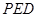 ;
;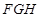 与平面
与平面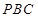 所成锐二面角的大小.
所成锐二面角的大小.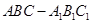 中,平面
中,平面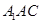 ⊥平面ABC,BC⊥AC,D为AC的中点,AC=BC=AA1=A1C=2。
⊥平面ABC,BC⊥AC,D为AC的中点,AC=BC=AA1=A1C=2。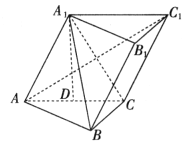
 中,
中,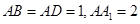 ,点
,点 为
为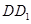 的中点.
的中点.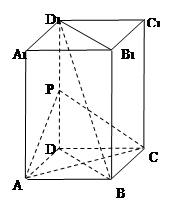
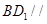 平面
平面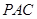 ;
;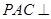 平面
平面 ;
;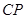 与平面
与平面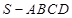 的底面是正方形,
的底面是正方形,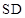 ⊥平面
⊥平面 ,
,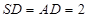
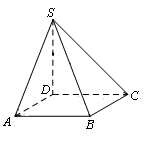
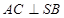 ;
;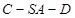 的大小.
的大小.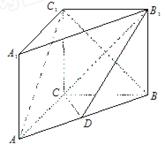
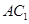 ∥平面
∥平面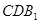 ;
;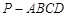 中,底面
中,底面 是平行四边形,
是平行四边形, 平面
平面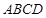 ,垂足为
,垂足为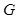 ,
,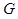 在
在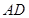 上且
上且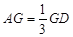 ,
,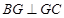 ,
,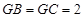 ,
,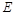 是
是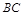 的中点,四面体
的中点,四面体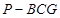 的体积为
的体积为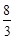 .
.
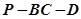 的正切值;
的正切值; 到平面
到平面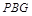 所成角的正弦值;
所成角的正弦值;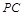 上是否存在一点
上是否存在一点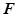 ,使异面直线
,使异面直线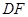 与
与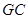 所成的角为
所成的角为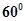 ,若存在,确定点
,若存在,确定点