题目内容
如图,四边形 是正方形,
是正方形, 平面
平面 ,
,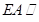
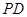 ,
,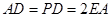 ,
,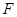 ,
,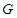 ,
, 分别为
分别为 ,
,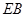 ,
, 的中点.
的中点.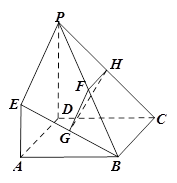
(1)求证: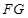
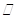 平面
平面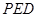 ;
;
(2)求平面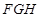 与平面
与平面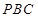 所成锐二面角的大小.
所成锐二面角的大小.
(1)证明详见解答;(2)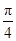 (或
(或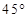 ).
).
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
如图,四边形 是正方形,
是正方形, 平面
平面 ,
,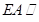
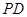 ,
,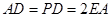 ,
,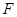 ,
,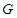 ,
, 分别为
分别为 ,
,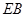 ,
, 的中点.
的中点.
(1)求证: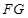
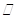 平面
平面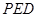 ;
;
(2)求平面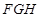 与平面
与平面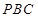 所成锐二面角的大小.
所成锐二面角的大小.
(1)证明详见解答;(2)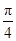 (或
(或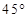 ).
).
解析

 阅读快车系列答案
阅读快车系列答案