题目内容
17.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),右焦点为F,点B为短轴的一个端点,O为坐标原点,若∠BFO=30°,且椭圆上任意一点到点F的最短距离为2-$\sqrt{3}$.(1)求椭圆C的标准方程;
(2)过点P(1,2)作椭圆C的切线,求切线方程.
分析 (1)由题意列出关于a,c的方程组,求解方程组得a,c的值,代入隐含条件求得b,则椭圆方程可求;
(2)设出切点,得到关于切点坐标的方程,再由切点在椭圆上得另一方程,联立方程组求得切点坐标,则椭圆的切线方程可求.
解答 解:(1)如图,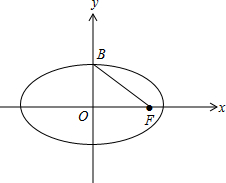
由题意可得,a=2b,且a-c=2-$\sqrt{3}$,
又a2=b2+c2,得a=2,c=$\sqrt{3}$.
∴椭圆C的标准方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)由题意,设过点P(1,2)的椭圆的切线与椭圆的切点为(x0,y0),
则$\frac{{x}_{0}}{4}+\frac{2{y}_{0}}{3}=1$,
又$\frac{{{x}_{0}}^{2}}{4}+\frac{{{y}_{0}}^{2}}{3}=1$,
联立$\left\{\begin{array}{l}{\frac{{x}_{0}}{4}+\frac{2{y}_{0}}{3}=1}\\{\frac{{{x}_{0}}^{2}}{4}+\frac{{{y}_{0}}^{2}}{3}=1}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{x}_{0}=\frac{12+8\sqrt{7}}{19}}\\{{y}_{0}=\frac{24-3\sqrt{7}}{19}}\end{array}\right.$或$\left\{\begin{array}{l}{{x}_{0}=\frac{12-8\sqrt{7}}{19}}\\{{y}_{0}=\frac{24+3\sqrt{7}}{19}}\end{array}\right.$.
∴所求企切线方程为:$(9+6\sqrt{7})x+(48-6\sqrt{7})y-57=0$,或$(9-6\sqrt{7})x+(48+6\sqrt{7})y-57=0$.
点评 本题考查椭圆标准方程的求法,考查了椭圆切线方程的求法,设出过椭圆外一点的切线方程是解答该题的关键,考查了计算能力,是中档题.

 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案| A. | (0,1),(1,2) | B. | {(0,1),(1,2)} | C. | {y|y=1或y=2} | D. | {y|y≥1} |
 如图1在直角三角形ABC中,∠A=90°,AB=2,AC=4,D,E分别是AC,BC边上的中点,M为CD的中点,现将△CDE沿DE折起,使点A在平面CDE内的射影恰好为M.
如图1在直角三角形ABC中,∠A=90°,AB=2,AC=4,D,E分别是AC,BC边上的中点,M为CD的中点,现将△CDE沿DE折起,使点A在平面CDE内的射影恰好为M.