题目内容
7.已知S是边长为a的等边三角形ABC所在平面外一点,SA=SB=SC,D为AB的中点,且SD与BC所成的角为45°,求SD与平面ABC所成角的正弦值.分析 取AC的中点E,连接DE,SE,则DE∥BC,可得∠SDE=45°,求出SD=$\frac{\sqrt{2}}{4}$a,S在三角形ABC中的射影为三角形ABC的中心O,再求出SO,即可求出SD与平面ABC所成角的正弦值.
解答 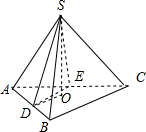 解:取AC的中点E,连接DE,SE,则DE∥BC,
解:取AC的中点E,连接DE,SE,则DE∥BC,
∵SD与BC所成的角为45°,
∴∠SDE=45°,
∵SD=SE,
∴DE=$\sqrt{2}$SD,
∴SD=$\frac{\sqrt{2}}{4}$a,
∵S是边长为a的等边三角形ABC所在平面外一点,SA=SB=SC,
∴S在三角形ABC中的射影为三角形ABC的中心O,
∵OD=$\frac{\sqrt{3}}{6}$a,
∴SO=$\frac{\sqrt{6}}{12}$a,
∴SD与平面ABC所成角的正弦值为$\frac{\frac{\sqrt{6}}{12}a}{\frac{\sqrt{2}}{4}a}$=$\frac{\sqrt{3}}{3}$.
点评 本题考查线面角,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目