题目内容
设f(n)=1+ +
+ + +
+ + (n∈N*).
(n∈N*).
求证:f(1)+f(2)+ +f(n-1)=n·[f(n)-1](n≥2,n∈N*).
应用数学归纳法.
解析试题分析:①当n=2时,左边=f(1)=1,
右边=2[1+ -1]=1,
-1]=1,
左边=右边,等式成立.
②假设n=k时,结论成立,即
f(1)+f(2)+ +f(k-1)=k[f(k)-1],
那么,当n=k+1时,
f(1)+f(2)+ +f(k-1)+f(k)
=k[f(k)-1]+f(k)
=(k+1)f(k)-k
=(k+1)[f(k+1)- ]-k
]-k
=(k+1)f(k+1)-(k+1)=(k+1)[f(k+1)-1],
所以当n=k+1时结论仍然成立.
所以f(1)+f(2)+ +f(n-1)=n[f(n)-1](n≥2,n∈N*).
考点:本题主要考查数学归纳法。
点评:中档题,利用数学归纳法,注意遵循“两步一结”。对数学式子变形能力要求较高。

练习册系列答案
相关题目
若x+yi=1+2xi(x,y∈R),则x﹣y等于( )
| A.0 | B.﹣1 | C.1 | D.2 |
设点 对应的复数为
对应的复数为 ,以原点为极点,实轴正半轴为极轴建立极坐标系,
,以原点为极点,实轴正半轴为极轴建立极坐标系,
则点 的极坐标可能为( )
的极坐标可能为( )
A.(3, ) ) | B.(3, ) ) | C.( , , ) ) | D.( , , ) ) |
已知 为虚数单位,复数
为虚数单位,复数 ,则复数
,则复数 的虚部是( )
的虚部是( )
A. | B. | C. | D. |
 ;
; ,试用分析法证明:
,试用分析法证明: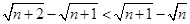 .
. +
+ +…+
+…+ =
= (n∈N*).
(n∈N*). 是等差数列,
是等差数列, 设
设 N+),
N+), N+),问Pn与Qn哪一个大?并证明你的结论.
N+),问Pn与Qn哪一个大?并证明你的结论. ;
; ;
; ,
,