题目内容
请观察以下三个式子:
① ;
;
② ;
;
③ ,
,
归纳出一般的结论,并用数学归纳法证明之.

证明:①当 ,左边=3,右边=3,
,左边=3,右边=3, 左边=右边
左边=右边
②假设当 时,命题成立,
时,命题成立,
即
则当 时
时

 当
当 时命题成立,由(1)、(2)知,命题成立.
时命题成立,由(1)、(2)知,命题成立.
解析试题分析: 3分
3分
证明:①当 ,左边=3,右边=3,
,左边=3,右边=3, 左边=右边
左边=右边
②假设当 时,命题成立,
时,命题成立,
即
则当 时
时

 当
当 时命题成立,由(1)、(2)知,命题成立. 10分
时命题成立,由(1)、(2)知,命题成立. 10分
考点:本题考查了数学归纳法的运用
点评:运用数学归纳法证明有关命题要注意以下几点:(1)数学归纳法的两步分别是数学归纳法的两个必要条件,二者缺一不可,两步均得以证明才具备了充分性。(2)第二步中,证明“当n=k+1时结论也正确”,必须利用归纳假设,即必须用上“当n=k(k∈N※,k≥n0)时结论正确”这一条件。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设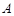 是由
是由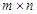 个实数组成的
个实数组成的 行
行 列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
(Ⅰ) 数表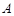 如表1所示,若经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负实数,请写出每次“操作”后所得的数表(写出一种方法即可);
如表1所示,若经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负实数,请写出每次“操作”后所得的数表(写出一种方法即可);
表1
| 1 | 2 | 3 |  |
 | 1 | 0 | 1 |
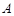 如表2所示,若必须经过两次“操作”,才可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数
如表2所示,若必须经过两次“操作”,才可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数 的所有可能值;
的所有可能值;表2

(Ⅲ)对由
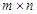 个实数组成的
个实数组成的 行
行 列的任意一个数表
列的任意一个数表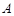 ,能否经过有限次“操作”以后,使得到的数表每行的各数之和与每列的各数之和均为非负整数?请说明理由.
,能否经过有限次“操作”以后,使得到的数表每行的各数之和与每列的各数之和均为非负整数?请说明理由. 若x+yi=1+2xi(x,y∈R),则x﹣y等于( )
| A.0 | B.﹣1 | C.1 | D.2 |
已知复数  ,则复数z的共轭复数在复平面内对应的点在
,则复数z的共轭复数在复平面内对应的点在
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
设 为虚数单位,若复数
为虚数单位,若复数 为纯虚数,则实数
为纯虚数,则实数 的值为( )
的值为( )
A. | B. | C. | D. |
复数 = ( )
= ( )
A. | B. | C. | D. |
 满足:集合
满足:集合 中至少存在三个不同的数构成等比数列,则称函数
中至少存在三个不同的数构成等比数列,则称函数 ;②
;② 中,哪些是等比源函数?(不需证明)
中,哪些是等比源函数?(不需证明) ,函数
,函数 不是等比源函数;
不是等比源函数; ,函数
,函数 都是等比源函数.
都是等比源函数. +
+ ≥
≥ .
. +
+ + +
+ + (n∈N*).
(n∈N*).