题目内容
求证:12-22+32-42+…+(2n-1)2-(2n)2=-n(2n+1)(n∈N*).
利用数学归纳法来证明与自然数相关的命题,分为两步来进行。
解析试题分析:证明: ①n=1时,左边=12-22=-3,右边=-3,等式成立.
②假设n=k时,等式成立,即12-22+32-42+…+(2k-1)2-(2k)2=-k(2k+1)2.
当n=k+1时,12-22+32-42+…+(2k-1)2-(2k)2+(2k+1)2-(2k+2)2=-k(2k+1)+(2k+1)2-(2k+2)2=-k(2k+1)-(4k+3)=-(2k2+5k+3)=-(k+1)[2(k+1)+1],所以n=k+1时,等式也成立.
由①②得,等式对任何n∈N*都成立.
考点:数学归纳法
点评:主要是考查了数学归纳法的运用,分为两步骤来进行,属于基础题。

练习册系列答案
相关题目
已知复数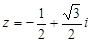 ,则
,则 =( )
=( )
A. | B.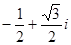 | C.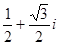 | D. |
已知 为虚数单位,
为虚数单位, ,若
,若 是纯虚数,则
是纯虚数,则 的值为( )
的值为( )
| A.-1或1 | B.1 | C.3 | D.-1 |
 (
( )
) 均为实数,且
均为实数,且 ,
, ,
, 求证:
求证: .
.

 +
+ + +
+ + (n∈N*).
(n∈N*). 中,
中, 、
、 ,且
,且 .
. 、
、 ,猜想
,猜想 的表达式,并加以证明;
的表达式,并加以证明; ,求证:对任意的自然数
,求证:对任意的自然数 ,都有
,都有 .
.