题目内容
 如图,椭圆
如图,椭圆| x2 |
| a2 |
| y2 |
| b2 |
(Ⅰ)已知椭圆短轴的两个三等分点与一个焦点构成正三角形,求椭圆的方程;
(Ⅱ)点M是直线l:x=4上的动点,以OM为直径的圆过点N,且NF⊥OM,是否存在一个定点,使得N到该定点的距离为定值?并说明理由.
分析:(Ⅰ)根据椭圆短轴的两个三等分点与一个焦点构成正三角形,得到椭圆短轴的三分之一的值,由此列式可以得到椭圆的半短轴的长,结合a2=b2+c2可以得到a2的值,所以椭圆方程可求;
(Ⅱ)设出N的坐标,求出NF所在直线的斜率,由NF⊥OM得到OM所在直线的斜率,写出OM所在直线方程后得到M点的坐标,求出ON和MN的斜率,由以OM为直径的圆过点N,得到ON和MN所在直线的斜率之积等于-1,列式整理后即可得到结论.
(Ⅱ)设出N的坐标,求出NF所在直线的斜率,由NF⊥OM得到OM所在直线的斜率,写出OM所在直线方程后得到M点的坐标,求出ON和MN的斜率,由以OM为直径的圆过点N,得到ON和MN所在直线的斜率之积等于-1,列式整理后即可得到结论.
解答: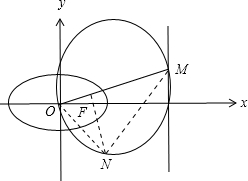 解:(Ⅰ)因为椭圆短轴的两个三等分点与一个焦点构成正三角形,且c=1,
解:(Ⅰ)因为椭圆短轴的两个三等分点与一个焦点构成正三角形,且c=1,
所以
=
×2b,解得b=
.
∴a2=b2+c2=4.
∴椭圆的方程为
+
=1;
(Ⅱ)存在定点O(原点),使得N到该定点的距离为定值,如图,
设N(x0,y0),则直线NF的斜率为kNF=
,
直线ON的斜率为kON=
∵NF⊥OM,∴直线OM的斜率为kOM=-
,
∴直线OM的方程为y=-
x,点M的坐标为M(4,-
).
∴直线MN的斜率为kMN=
.
∵ON⊥MN,∴kMN•kON=-1,∴
•
=-1,
整理得x02+y02=4.
∴存在定点O(原点),使得N到该定点的距离为定值,且该定值为2.
 解:(Ⅰ)因为椭圆短轴的两个三等分点与一个焦点构成正三角形,且c=1,
解:(Ⅰ)因为椭圆短轴的两个三等分点与一个焦点构成正三角形,且c=1,所以
2
| ||
| 3 |
| 1 |
| 3 |
| 3 |
∴a2=b2+c2=4.
∴椭圆的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)存在定点O(原点),使得N到该定点的距离为定值,如图,
设N(x0,y0),则直线NF的斜率为kNF=
| y0 |
| x0-1 |
直线ON的斜率为kON=
| y0 |
| x0 |
∵NF⊥OM,∴直线OM的斜率为kOM=-
| x0-1 |
| y0 |
∴直线OM的方程为y=-
| x0-1 |
| y0 |
| 4(x0-1) |
| y0 |
∴直线MN的斜率为kMN=
y0+
| ||
| x0-4 |
∵ON⊥MN,∴kMN•kON=-1,∴
y0+
| ||
| x0-4 |
| y0 |
| x0 |
整理得x02+y02=4.
∴存在定点O(原点),使得N到该定点的距离为定值,且该定值为2.
点评:本题考查了椭圆的标准方程和简单几何性质,考查了直线和圆锥曲线的关系,考查了数学转化思想方法和数形结合的解题思想,考查了学生的计算能力,是有一定难度题目.

练习册系列答案
相关题目
 如图,椭圆
如图,椭圆 如图,椭圆
如图,椭圆 如图,椭圆
如图,椭圆 (2010•武清区一模)如图,椭圆
(2010•武清区一模)如图,椭圆 如图,椭圆
如图,椭圆