题目内容
命题p：?x∈R，3x＞x；命题q：若函数y=f（x-3）为奇函数，则函数y=f（x）的图象关于点（3，0）成中心对称．下列命题正确的是（ ）
分析：分别求出命题p，q成立的等价条件，利用复合命题与简单命题之间的关系，进行判断．
解答：解：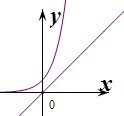
由指数函数和一次函数的图象可知，?x∈R，3x＞x恒成立，即命题p为真命题．
若函数y=f（x-3）为奇函数，则函数y=f（x-3）关于原点（0，0）对称，将函数y=f（x-3）向左平移3个单位得到y=f（x）的图象，
则函数y=f（x）的图象关于点（-3，0）成中心对称，所以q为假命题．
所以p∨q为真，p∧q为假，￢p为假，￢q为真．
故选A．
由指数函数和一次函数的图象可知，?x∈R，3x＞x恒成立，即命题p为真命题．若函数y=f（x-3）为奇函数，则函数y=f（x-3）关于原点（0，0）对称，将函数y=f（x-3）向左平移3个单位得到y=f（x）的图象，
则函数y=f（x）的图象关于点（-3，0）成中心对称，所以q为假命题．
所以p∨q为真，p∧q为假，￢p为假，￢q为真．
故选A．
点评：本题主要考查复合命题与简单命题之间的关系，利用条件先求出p，q成立的等价条件是解决此类问题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目