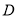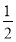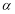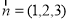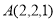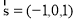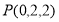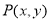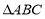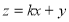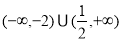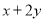题目内容
已知定点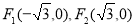 ,曲线C是使
,曲线C是使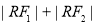 为定值的点
为定值的点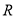 的轨迹,曲线
的轨迹,曲线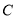 过点
过点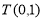 .
.
(1)求曲线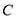 的方程;
的方程;
(2)直线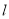 过点
过点 ,且与曲线
,且与曲线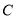 交于
交于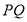 ,当
,当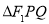 的面积取得最大值时,求直线
的面积取得最大值时,求直线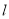 的方程;
的方程;
(3)设点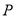 是曲线
是曲线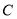 上除长轴端点外的任一点,连接
上除长轴端点外的任一点,连接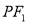 、
、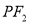 ,设
,设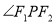 的角平分线
的角平分线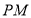 交曲线
交曲线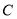 的长轴于点
的长轴于点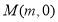 ,求
,求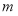 的取值范围.
的取值范围.
(1)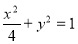 ;(2)
;(2)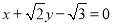 和
和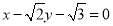 ;(3)
;(3)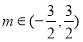 .
.
【解析】
试题分析:(1)依题意并结合椭圆的定义,先判断出曲线 的轨迹是以原点为中心,以
的轨迹是以原点为中心,以 为焦点的椭圆,从而得出椭圆中参数
为焦点的椭圆,从而得出椭圆中参数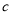 的值,由
的值,由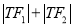 计算出参数
计算出参数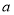 的值,最后由
的值,最后由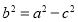 计算出
计算出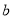 的取值即可得到曲线
的取值即可得到曲线 的方程;(2)设点
的方程;(2)设点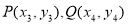 ,联立直线与椭圆的方程,消去
,联立直线与椭圆的方程,消去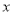 得到
得到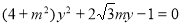 ,从而由二次方程根与系数的关系得到
,从而由二次方程根与系数的关系得到 ,再由弦长公式计算出
,再由弦长公式计算出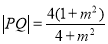 ,再计算出点
,再计算出点 到直线
到直线 的距离
的距离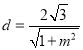 ,由公式
,由公式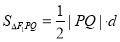 计算出三角形的面积(含参数
计算出三角形的面积(含参数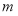 ),结合基本不等式可确定面积最大时的
),结合基本不等式可确定面积最大时的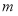 值,从而可确定直线方程;(3)设
值,从而可确定直线方程;(3)设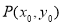 ,由角平分线可得
,由角平分线可得 =
=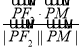 ,化简并代入坐标进行运算,即可得出
,化简并代入坐标进行运算,即可得出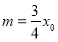 ,然后根据
,然后根据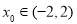 ,可确定
,可确定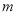 的取值范围.
的取值范围.
试题解析:(1)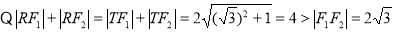 2分
2分
 曲线C为以原点为中心,
曲线C为以原点为中心, 为焦点的椭圆
为焦点的椭圆
设其长半轴为 ,短半轴为
,短半轴为 ,半焦距为
,半焦距为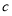 ,则
,则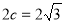 ,
,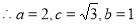
 曲线C的方程为
曲线C的方程为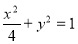 4分
4分
(2)设直线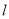 的为
的为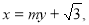 代入椭圆方程
代入椭圆方程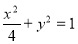 ,得
,得
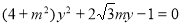 ,计算并判断得
,计算并判断得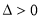 ,
,
设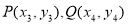 ,得
,得

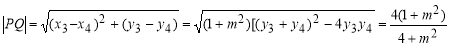
 到直线
到直线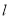 的距离
的距离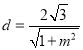 ,设
,设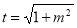 ,则
,则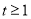

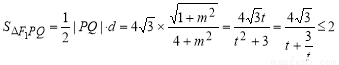
当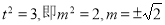 时,面积最大
时,面积最大

 的面积取得最大值时,直线l的方程为:
的面积取得最大值时,直线l的方程为:
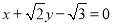 和
和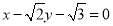 9分
9分
(3)由题意可知: =
=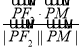 ,
,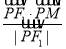 =
=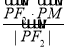 10分
10分
设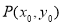 其中
其中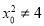 ,将向量坐标代入并化简得:
,将向量坐标代入并化简得:
m(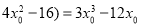 , 12分
, 12分
因为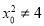 ,所以
,所以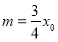 , 13分
, 13分
而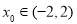 ,所以
,所以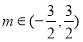 14分
14分
考点:1.轨迹问题;2.椭圆及其标准方程;3.直线与圆锥曲线的综合问题.

练习册系列答案
相关题目