题目内容
过点 且与圆
且与圆 相切的直线方程为_________________
相切的直线方程为_________________
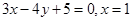
解析试题分析:根据题意,圆心(0,0),半径为1,那么可知过点(1,0)斜率不存在时则可知x=1符合题意,同时当斜率存在时,则利用圆心到直线的距离为半径1,即设直线方程为y-2=k(x-1),结合点到直线的距离公式,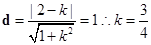 ,则可知直线方程为
,则可知直线方程为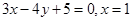
考点:直线方程
点评:解决的关键是根据直线与圆相切的思想利用直线的垂直关系来得到直线方程的求解。

练习册系列答案
相关题目
题目内容
过点 且与圆
且与圆 相切的直线方程为_________________
相切的直线方程为_________________
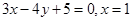
解析试题分析:根据题意,圆心(0,0),半径为1,那么可知过点(1,0)斜率不存在时则可知x=1符合题意,同时当斜率存在时,则利用圆心到直线的距离为半径1,即设直线方程为y-2=k(x-1),结合点到直线的距离公式,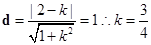 ,则可知直线方程为
,则可知直线方程为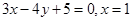
考点:直线方程
点评:解决的关键是根据直线与圆相切的思想利用直线的垂直关系来得到直线方程的求解。
