题目内容
【题目】已知f(x)为定义在R上的奇函数,且当x≥0时,f(x)=x2﹣(a+4)x+a.
(1)求实数a的值及f(x)的解析式;
(2)求使得f(x)=x+6成立的x的值.
【答案】
(1)解:∵f(x)为定义在R上的奇函数,
∴f(0)=a=0,
由题意x≥0时:f(x)=x2﹣4x,
设x<0,则﹣x>0,
则f(﹣x)=x2+4x=﹣f(x),
故x<0时,f(x)=﹣x2﹣4x,
故f(x)= 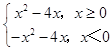
(2)解:当x≥0时,x2﹣4x=x+6,可得x=6;
x<0时,f(x)=﹣x2﹣4x=x+6,可得x=﹣2或﹣3.
综上所述,方程的解为6,﹣2或﹣3
【解析】(1)根据函数的奇偶性得到f(0)=0,求出a的值即可;令﹣x>0,得到x<0,根据函数的奇偶性求出函数的解析式即可;(2)根据函数解析式,建立方程,即可得出结论.

练习册系列答案
相关题目