题目内容
【题目】已知等差数列{an}的公差为2，前n项和为Sn ， 且S1、S2、S4成等比数列．
（1）求数列{an}的通项公式；
（2）令bn=（﹣1）n﹣1 
，求数列{bn}的前n项和Tn ．
【答案】
（1）解：∵等差数列{an}的公差为2，前n项和为Sn，且S1、S2、S4成等比数列．
∴Sn=na1+n（n﹣1）
（2a1+2）2=a1（4a1+12），a1=1，
∴an=2n﹣1
（2）解：∵由（Ⅰ）可得bn=（﹣1）n﹣1 
=（﹣1）n﹣1 
=（﹣1）n﹣1（ 
+ 
）．
∴Tn=（1+ 
）﹣（ + 
）+（ + 
）+…+（﹣1）n﹣1（ + ）．
当n为偶数时，Tn=1+ ）﹣（ + ）+（ + ）+…+（ 
+ ）﹣（ + ）=1﹣ = 
．
当n为奇数时，Tn=1+ ）﹣（ + ）+（ + ）+…﹣（ + ）+（ + ）=1+ = 
．
∴Tn=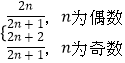 
．
【解析】（1）根据等差数列的性质得出（2a1+2）2=a1（4a1+12），a1=1，运用通项公式求解即可．（2）由（Ⅰ）可得bn=（﹣1）n﹣1（ + ）．对n分类讨论“裂项求和”即可得出
【考点精析】利用数列的前n项和对题目进行判断即可得到答案，需要熟知数列{an}的前n项和sn与通项an的关系
．
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
【题目】某同学用“五点法”画函数f（x）=Asin（ωx+φ）（ω＞0，|φ|＜ 
）在某一个周期内的图象时，列表并填入了部分数据，如表：
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
Asin（ωx+φ） | 0 | 2 | ﹣2 | 0 |
（1）请将上表数据补充完整，并直接写出函数f（x）的解析式；
（2）将函数y=f（x）的图象向左平移 
个单位后，再将得到的图象上各点的横坐标伸长到原来的4倍，纵坐标不变，得到函数y=g（x）的图象，求g（x）的单调递减区间．
