题目内容
【题目】设等比数列{an}的前n项和为Sn , 已知a1=2,且4S1 , 3S2 , 2S3成等差数列. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=|2n﹣5|an , 求数列{bn}的前n项和Tn .
【答案】解:(Ⅰ)∵4S1 , 3S2 , 2S3成等差数列, ∴6S2=4S1+2S3 ,
即6(a1+a2)=4a1+2(a1+a2+a3),
则:a3=2a2 , q=2,
∴ ![]() ;
;
(Ⅱ)当n=1,2时,T1=6,T2=10,
当n≥3,Tn=10+1×23+3×24+…+(2n﹣5)2n ,
2Tn=20+1×24+3×25+…+(2n﹣7)×2n+(2n﹣5)×2n+1 ,
两式相减得:﹣Tn=﹣10+8+2(24+25+…+2n)﹣(2n﹣5)×2n+1 ,
=﹣2+2× ![]() ﹣(2n﹣5)×2n+1 ,
﹣(2n﹣5)×2n+1 ,
=﹣34+(7﹣2n)2n+1 ,
∴Tn=34﹣(7﹣2n)2n+1 .
∴ 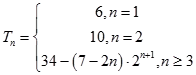 .
.
【解析】(Ⅰ)根据4S1 , 3S2 , 2S3成等差数列.根据等差中项6S2=4S1+2S3 , 化简整理求得q=2,写出通项公式;(Ⅱ)讨论当n=1、2时,求得T1=6,T2=10,写出前n项和,采用错位相减法求得Tn .

 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案【题目】已知函数f(x)=2x+2ax(a为实数),且f(1)= ![]() .
.
(1)求函数f(x)的解析式;
(2)判断函数f(x)的奇偶性并证明;
(3)判断函数f(x)在区间[0,+∞)的单调性,并用定义证明.
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|< ![]() )在某一个周期内的图象时,列表并填入了部分数据,如表:
)在某一个周期内的图象时,列表并填入了部分数据,如表:
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx+φ) | 0 | 2 | ﹣2 | 0 |
(1)请将上表数据补充完整,并直接写出函数f(x)的解析式;
(2)将函数y=f(x)的图象向左平移 ![]() 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.