题目内容
(本小题满分12分)
已知函数f (x)=alnx+x2 (a为实常数).[来源:ZXXK][来源:学*科*网Z*X*X*K]
(Ⅰ)若a=-2,求证:函数f (x)在(1,+∞)上是增函数;
(Ⅱ)求函数f (x)在[1,e]上的最小值及相应的x值;
(Ⅲ)若当x∈[1,e]时,f (x)≤(a+2)x恒成立,求实数a的取值范围.
(1)略;(2)e;(3)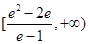
【解析】(1)当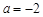 时,
时,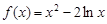 ,
,
当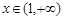 ,
,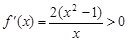 ,
,
故函数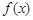 在
在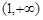 上是增函数.
…………2分
上是增函数.
…………2分
(2)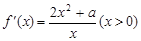 ,
,
当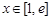 ,
,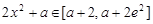 .
.
若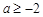 ,
,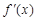 在
在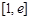 上非负(仅当
上非负(仅当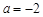 ,x=1时,
,x=1时,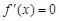 ),
),
故函数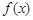 在
在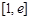 上是增函数,
上是增函数,
此时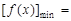
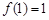 .
…………4分
.
…………4分
若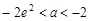 ,当
,当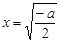 时,
时,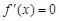 ;
;
当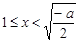 时,
时,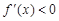 ,
,
此时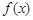 是减函数;
是减函数;
当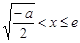 时,
时,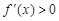 ,
,
此时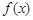 是增函数.
是增函数.
故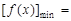
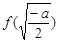
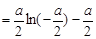 .
…………6分[来源:Zxxk.Com]
.
…………6分[来源:Zxxk.Com]
若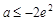 ,
,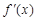 在
在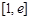 上非正(仅当
上非正(仅当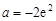 ,x=e时,
,x=e时,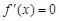 ),
),
故函数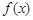 在
在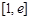 上是减函数,
上是减函数,
此时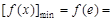
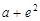 .
…………7分
.
…………7分
综上可知,当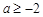 时,
时,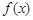 的最小值为1,相应的x值为1;
的最小值为1,相应的x值为1;
当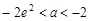 时,
时,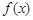 的最小值为
的最小值为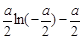 ,[来源:学§科§网Z§X§X§K]
,[来源:学§科§网Z§X§X§K]
相应的x值为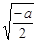 ;
;
当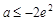 时,
时,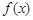 的最小值为
的最小值为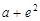 ,相应的x值为
,相应的x值为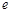 . …………8分[来源:学.科.网]
. …………8分[来源:学.科.网]
(3)不等式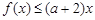 ,
,
可化为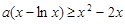 .
.
∵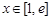 , ∴
, ∴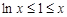 且等号不能同时取,
且等号不能同时取,
所以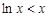 ,即
,即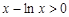 ,
,
因而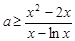 (
(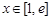 )
…………9分
)
…………9分
令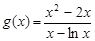 (
(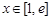 ),
),
又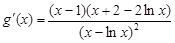 , …………10分
, …………10分
当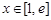 时,
时,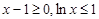 ,
,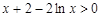 ,
,
从而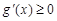 (仅当x=1时取等号),
(仅当x=1时取等号),
所以 在
在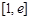 上为增函数, …………11分
上为增函数, …………11分
故 的最大值为
的最大值为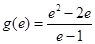 ,
,
所以a的取值范围是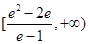 . ……12分
. ……12分

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案