题目内容
下列四种说法:(1)命题:“存在x∈R,使得x2+1>3x”的否定是“对任意x∈R,都有x2+1≤3x”.
(2)若直线a、b在平面α内的射影互相垂直,则a⊥b.
(3)已知一组数据为20、30、40、50、60、70,则这组数据的众数、中位数、平均数的大小关系是:众数>中位数>平均数.
(4)已知回归方程
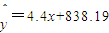 ,则可估计x与y的增长速度之比约为
,则可估计x与y的增长速度之比约为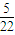 .
.(5)若A(-2,3),B(3,-2),C(
 ,m)三点共线,则m的值为2.
,m)三点共线,则m的值为2.其中所有正确说法的序号是 .
【答案】分析:利用含量词的命题的否定形式判断出(1)对;据画出直线的位置关系判断出(2)错;据数据特征数的求法判断出(3)错;给x增加一个单位据回归直线方程求出y的变化量,求出x与y的增长速度之比,判断出(4)错;据三点共线转化为两向量共线,利用向量共线的充要条件求出m的范围,判断出(5)错.
解答:解:对于(1)根据含量词的命题的否定,将量词交换同时将结论否定,得到(1)对
对于(2)当两条直线斜交时,两直线在同一个平面的射影也有可能垂直,故(2)错
对于(3)这组数据的众数为20,30,40,50,60,70共6个值,中位数为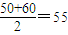 ,
,
平均数为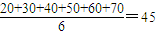 故(3)错
故(3)错
对于(4)x每增加一个单位,y平均增加4,.4,所以x与y的增长速度之比约为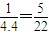 ,故(4)对
,故(4)对
对于(5)A、B、C三点共线,则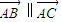
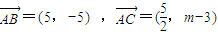 ,∴
,∴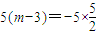 ,∴
,∴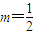 故(5)错
故(5)错
故答案为(1)(4)
点评:解决含量词的命题的否定,只需将量词互换,结论否定即可;解决三点共线问题常转化为两个向量共线问题,利用向量关系的充要条件来解决.
解答:解:对于(1)根据含量词的命题的否定,将量词交换同时将结论否定,得到(1)对
对于(2)当两条直线斜交时,两直线在同一个平面的射影也有可能垂直,故(2)错
对于(3)这组数据的众数为20,30,40,50,60,70共6个值,中位数为
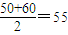 ,
,平均数为
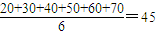 故(3)错
故(3)错对于(4)x每增加一个单位,y平均增加4,.4,所以x与y的增长速度之比约为
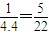 ,故(4)对
,故(4)对对于(5)A、B、C三点共线,则
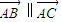
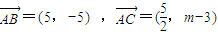 ,∴
,∴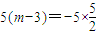 ,∴
,∴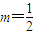 故(5)错
故(5)错故答案为(1)(4)
点评:解决含量词的命题的否定,只需将量词互换,结论否定即可;解决三点共线问题常转化为两个向量共线问题,利用向量关系的充要条件来解决.

练习册系列答案
相关题目
 某工厂12年来某产品总产量S与时间t(年)的函数关系如图所示,下列四种说法:
某工厂12年来某产品总产量S与时间t(年)的函数关系如图所示,下列四种说法: