题目内容
下列四种说法：
（1）不等式（x-1）
≥0的解集为[2，+∞）；
（2）若a，b∈R，则“log3a＞log3b”是“(
)a＜(
)b”成立的必要不充分条件；
（3）把函数y=sin（-2x）（x∈R）的图象上所有的点向右平移
个单位即可得到函数
y=sin(-2x+
)(x∈R)的图象；
（4）函数f(x)=log
(x2+ax+2)的值域为R，则实数a的取值范围是（-2
，2
）．
其中正确的说法有（ ）
（1）不等式（x-1）
| x2-x-2 |
（2）若a，b∈R，则“log3a＞log3b”是“(
| 1 |
| 3 |
| 1 |
| 3 |
（3）把函数y=sin（-2x）（x∈R）的图象上所有的点向右平移
| π |
| 8 |
y=sin(-2x+
| π |
| 4 |
（4）函数f(x)=log
| 1 |
| 2 |
| 2 |
| 2 |
其中正确的说法有（ ）
| A、.1个 | B、2个 |
| C、3个 | D、.4个 |
分析：（1）由x2-x-2≥0可知x-1≥0，但要注意x2≥-x-2=0时，x-1可任意取值．
（2）结合指对函数的单调性求解，对数函数的真数大于0
（3）图象的平移问题符合“左加右减”的原则，但是在x上变化多少．
（4）值域为R，需要△≥0，而不是△＜0
（2）结合指对函数的单调性求解，对数函数的真数大于0
（3）图象的平移问题符合“左加右减”的原则，但是在x上变化多少．
（4）值域为R，需要△≥0，而不是△＜0
解答：解：（1）中x=-1是不等式的一个解，故命题错误
（2）“log3a＞log3b”即a＞b＞0，而(
)a＜(
)b是a＞b，故命题错误
（3）把函数y=sin（-2x）（x∈R）的图象上所有的点向右平移
个单位即可得到
y=sin(-2(x-
))=sin(-2x+
)的图象，命题正确
（4）值域为R，需要△=a2-8≥0，解得-2
≤x≤2
，命题错误
故选A
（2）“log3a＞log3b”即a＞b＞0，而(
| 1 |
| 3 |
| 1 |
| 3 |
（3）把函数y=sin（-2x）（x∈R）的图象上所有的点向右平移
| π |
| 8 |
y=sin(-2(x-
| π |
| 8 |
| π |
| 4 |
（4）值域为R，需要△=a2-8≥0，解得-2
| 2 |
| 2 |
故选A
点评：本题以命题的真假判断为载体考查解不等式、指对函数的单调性应用、充要条件判断、图象变换等，综合性大，容易出现错误．
练习册系列答案
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
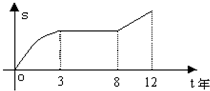某工厂12年来某产品总产量S与时间t（年）的函数关系如图所示，下列四种说法：