题目内容
【题目】已知椭圆
经过点
离心率
.
（Ⅰ）求椭圆的方程；
（Ⅱ）经过椭圆左焦点
的直线(不经过点
且不与
轴重合)与椭圆交于
两点，与直线
:
交于点
，记直线
的斜率分别为
.则是否存在常数
，使得向量
共线？若存在求出的值；若不存在，说明理由.
【答案】（1）
；（2）2.
【解析】
（1）根据椭圆
经过点
，离心率
，结合性质
，列出关于
、
、
的方程组，求出 、，即可得结果；（2）直线
的方程为
， 代入椭圆方程整理得
，求得
的坐标为
，求出
,利用韦达定理化简可得
，从而可得结果.
（1）由在椭圆上，
.①
由已知得
， 
又
， 
.②
②代入①解得
.
椭圆
的方程为.
（2）假设存在常数
，使得向量
共线，
，即
.
由题意可设的斜率为
，
则直线的方程为，③
代入椭圆方程
并整理，得，
设
，则有
，
.④
在方程③中令
得，的坐标为.
从而
，
，
.
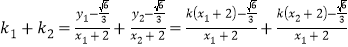
, ⑤
④代入⑤得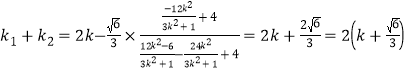
，
又
， .
故存在常数
符合题意.
【题目】某企业生产一种产品，从流水线上随机抽取100件产品，统计其质量指标值并绘制频率分布直方图（如图）：
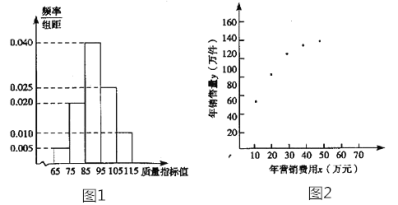
规定产品的质量指标值在
的为劣质品，在
的为优等品，在
的为特优品，销售时劣质品每件亏损1元，优等品每件盈利3元，特优品每件盈利5元.以这100 件产品的质量指标值位于各区间的频率代替产品的质量指标值位于该区间的概率.
（1）求每件产品的平均销售利润；
（2）该企业为了解年营销费用
（单位：万元）对年销售量
（单位：万件）的影响，对近5年年营销费用
和年销售量
数据做了初步处理，得到如图的散点图及一些统计量的值.
|
|
|
|
16.30 | 23.20 | 0.81 | 1.62 |
表中
，
，
，
.
根据散点图判断，
可以作为年销售量（万件）关于年营销费用（万元）的回归方程.
①求关于的回归方程；
⑦用所求的回归方程估计该企业应投人多少年营销费，才能使得该企业的年收益的预报值达到最大？（收益=销售利润营销费用，取
）
附：对于一组数据
，
，…，
其回归直线
均斜率和截距的最小二乘估计分别为
，
.
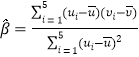【题目】随着中国教育改革的不断深入，越来越多的教育问题不断涌现.“衡水中学模式”入驻浙江，可以说是应试教育与素质教育的强烈碰撞.这一事件引起了广大市民的密切关注.为了了解广大市民关注教育问题与性别是否有关，记者在北京，上海，深圳随机调查了100位市民，其中男性55位，女性45位.男性中有45位关注教育问题，其余的不关注教育问题；女性中有30位关注教育问题，其余的不关注教育问题.
（1）根据以上数据完成下列2×2列联表；
关注教育问题 | 不关注教育问题 | 合计 | |||||
女 | 30 | 45 | |||||
男 | 45 | 55 | |||||
合计 |
| 100 | |||||
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | ||
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | ||
（2）能否在犯错误的概率不超过0.025的前提下认为是否关注教育与性别有关系？
参考公式：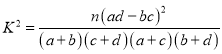
，其中
.
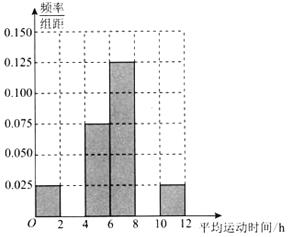
【题目】已知某企业有职工5000人，其中男职工3500人，女职工1500人．该企业为了丰富职工的业余生活，决定新建职工活动中心，为此，该企业工会采用分层抽样的方法，随机抽取了300名职工每周的平均运动时间（单位：h），汇总得到频率分布表（如表所示），并据此来估计该企业职工每周的运动时间：
平均运动时间 | 频数 | 频率 |
[0，2） | 15 | 0.05 |
[2，4） | m | 0.2 |
[4，6） | 45 | 0.15 |
[6，8） | 755 | 0.25 |
[8，10） | 90 | 0.3 |
[10，12） | p | n |
合计 | 300 | 1 |
（1）求抽取的女职工的人数；
（2）①根据频率分布表，求出m、n、p的值，完成如图所示的频率分布直方图，并估计该企业职工每周的平均运动时间不低于4h的概率；
男职工 | 女职工 | 总计 | |
平均运动时间低于4h | |||
平均运动时间不低于4h | |||
总计 |
②若在样本数据中，有60名女职工每周的平均运动时间不低于4h，请完成以下2×2列联表，并判断是否有95%以上的把握认为“该企业职工毎周的平均运动时间不低于4h与性别有关”．
附：K2=
，其中n=a+b+c+d．
P（K2≥k0） | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
