题目内容
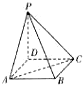如图，四棱锥P-ABCD的底面为正方形，PD⊥底面ABCD，PD=AD=1，设点CG到平面PAB的距离为d1，点B到平面PAC的距离为d2，则有（ ）分析：过C做平面PAB的垂线，垂足为E，连接BE，则三角形CEB为直角三角形，根据斜边大于直角边，再根据面PAC和面PAB与底面所成的二面角，能够推导出d2＜d1＜1．
解答：解：过C做平面PAB的垂线，
垂足为E，连接BE，
则三角形CEB为直角三角形，其中∠CEB=90°，
根据斜边大于直角边，得CE＜CB，即d2＜1．
同理，d1＜1．
再根据面PAC和面PAB与底面所成的二面角可知，前者大于后者，
所以d2＜d1．
所以d2＜d1＜1．
故选D．
垂足为E，连接BE，
则三角形CEB为直角三角形，其中∠CEB=90°，
根据斜边大于直角边，得CE＜CB，即d2＜1．
同理，d1＜1．
再根据面PAC和面PAB与底面所成的二面角可知，前者大于后者，
所以d2＜d1．
所以d2＜d1＜1．
故选D．
点评：本题考查空间距离的求法，解题时要认真审题，仔细解答，注意空间角的灵活运用．
练习册系列答案
相关题目
如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，
如图，四棱锥P-ABCD中，底面ABCD是直角梯形，AB∥CD，∠DAB=60°，AB=AD=2CD=2，侧面PAD⊥底面ABCD，且△PAD为等腰直角三角形，∠APD=90°，M为AP的中点．
如图，四棱锥P-ABCD的底面ABCD是矩形，AB=2，
如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥底面ABCD，且PA=AB=1，
如图，四棱锥P-ABCD，PA⊥平面ABCD，ABCD是直角梯形，DA⊥AB，CB⊥AB，PA=2AD=BC=2，AB=