题目内容
4.已知${a}^{\frac{1}{2}}$-${a}^{-\frac{1}{2}}$=3,求:(1)${a}^{\frac{1}{2}}$+${a}^{-\frac{1}{2}}$;
(2)${a}^{\frac{3}{2}}$-${a}^{-\frac{3}{2}}$.
分析 (1)由${a}^{\frac{1}{2}}$-${a}^{-\frac{1}{2}}$=3,可得${a}^{\frac{1}{2}}$+${a}^{-\frac{1}{2}}$=$\sqrt{({a}^{\frac{1}{2}}-{a}^{-\frac{1}{2}})^{2}+4}$.
(2)a+a-1=$({a}^{\frac{1}{2}}+{a}^{-\frac{1}{2}})^{2}$-2.可得${a}^{\frac{3}{2}}$-${a}^{-\frac{3}{2}}$=$({a}^{\frac{1}{2}}-{a}^{-\frac{1}{2}})$(a+a-1+1).
解答 解:(1)∵${a}^{\frac{1}{2}}$-${a}^{-\frac{1}{2}}$=3,∴${a}^{\frac{1}{2}}$+${a}^{-\frac{1}{2}}$=$\sqrt{({a}^{\frac{1}{2}}-{a}^{-\frac{1}{2}})^{2}+4}$=$\sqrt{{3}^{2}+4}$=$\sqrt{13}$.
(2)a+a-1=$({a}^{\frac{1}{2}}+{a}^{-\frac{1}{2}})^{2}$-2=13-2=11.
${a}^{\frac{3}{2}}$-${a}^{-\frac{3}{2}}$=$({a}^{\frac{1}{2}}-{a}^{-\frac{1}{2}})$(a+a-1+1)=3×(11+1)=36.
点评 本题考查了指数幂的运算性质、乘法公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.在等差数列{an}中,已知a1+a2+a3+a4+a5=11,a16+a17+a18+a19+a20=39,则S20=( )
| A. | 20 | B. | 50 | C. | 100 | D. | 150 |
15.已知函数g(x)=f(x)+x2是奇函数,且f(32)=-32,则f(-32)=( )
| A. | -2016 | B. | 2016 | C. | 32 | D. | -32 |
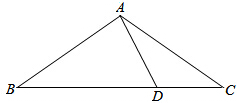 如图所示,在△ABC中,D是BC边上的一点,且BD=2DC,用$\overrightarrow{AB}$、$\overrightarrow{AC}$表示$\overrightarrow{AD}$.
如图所示,在△ABC中,D是BC边上的一点,且BD=2DC,用$\overrightarrow{AB}$、$\overrightarrow{AC}$表示$\overrightarrow{AD}$.