题目内容
10.在60°的二面角α-l-β,面α上一点到β的距离是2,那么这个点到棱的距离为( )| A. | $\frac{4\sqrt{3}}{3}$ | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
分析 A作AO⊥β垂足为O,作AH⊥l,垂足为H,连接HO,∠AHO为锐二面角α-l-β的平面角,在直角△AHO中求解即可.
解答 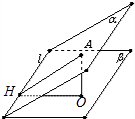 解:过A作AO⊥β垂足为O,则AO=2,作AH⊥l,垂足为H,连接HO,
解:过A作AO⊥β垂足为O,则AO=2,作AH⊥l,垂足为H,连接HO,
则l⊥OH,∠AHO为锐二面角α-l-β的平面角,
在直角△AHO中,sin∠AHO=$\frac{2}{AH}$=$\frac{\sqrt{3}}{2}$,
∴AH=$\frac{4\sqrt{3}}{3}$.
故选:A.
点评 本题考查二面角的大小度量,考查转化、空间想象、计算能力.本题找出∠AHO为锐二面角α-l-β的平面角是关键.

练习册系列答案
相关题目
20.某几何体的三视图如图所示,该几何体的体积是( )


| A. | a3 | B. | $\frac{3}{2}$a3 | C. | $\frac{1}{2}$a3 | D. | 3a3 |
18.某种产品的广告费用x与销售额y的统计数据如表:
(1)利用所给数据求广告费用x与销售额y之间的线性回归方程y=a+bx;
(2)预计在今后的销售中,销售额与广告费用还服从(1)中的关系,如果广告费用为6万元,请预测销售额为多少万元?
| 广告费用x(万元) | 1 | 2 | 3 | 4 | 5 |
| 销售额y(万元) | 10 | 12 | 15 | 18 | 20 |
(2)预计在今后的销售中,销售额与广告费用还服从(1)中的关系,如果广告费用为6万元,请预测销售额为多少万元?
8.已知某校5个学生的数学成绩和物理成绩如下表:
(1)通过大量事实证明发现,一个学生的数学成绩和物理成绩是具有很强的线性相关关系,用x表示数学成绩,用y表示物理成绩,求y关于x的回归方程;
(2)利用残差分析回归方程的拟合效果,若残差和在(-0.1,0.1)范围内,则称回归方程为“优拟方程”,问:该回归方程是否为“优拟方程”?
参考公式:残差和公式为:$\sum_{i=1}^{5}$(${y}_{i}-\widehat{{y}_{i}}$)).
| 学生的编号 | 1 | 2 | 3 | 4 | 5 |
| 数学成绩xi | 80 | 75 | 70 | 65 | 60 |
| 物理成绩yi | 70 | 66 | 68 | 64 | 62 |
(2)利用残差分析回归方程的拟合效果,若残差和在(-0.1,0.1)范围内,则称回归方程为“优拟方程”,问:该回归方程是否为“优拟方程”?
参考公式:残差和公式为:$\sum_{i=1}^{5}$(${y}_{i}-\widehat{{y}_{i}}$)).
 如图,设A是单位元和x轴正半轴的交点,P、Q是单位圆上的两点,O是坐标原点,∠AOP=$\frac{π}{6}$,∠POQ=α,α∈(0,π).
如图,设A是单位元和x轴正半轴的交点,P、Q是单位圆上的两点,O是坐标原点,∠AOP=$\frac{π}{6}$,∠POQ=α,α∈(0,π).