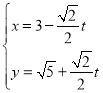题目内容
【题目】某市对全市高二学生的期末数学测试成绩统计显示,全市10000名学生的数学成绩服从正态分布![]() .现从甲校高二年级数学成绩在100分以上(含100分)的共200份试卷中用系统抽样的方法抽取了20份试卷进行分析(试卷编号为001,002,…,200),成绩统计如下:
.现从甲校高二年级数学成绩在100分以上(含100分)的共200份试卷中用系统抽样的方法抽取了20份试卷进行分析(试卷编号为001,002,…,200),成绩统计如下:
试卷编号 |
|
|
|
|
|
|
|
|
|
|
试卷得分 | 109 | 118 | 112 | 114 | 126 | 128 | 127 | 124 | 126 | 120 |
试卷编号 |
|
|
|
|
|
|
|
|
|
|
试卷得分 | 135 | 138 | 135 | 137 | 135 | 139 | 142 | 144 | 148 | 150 |
注:表中试卷编![]() .
.
(1)写出表中试卷得分为144分的试卷编号(写出具体数据即可);
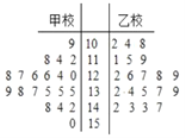
(2)该市又用系统抽样的方法从乙校中抽取了20份试卷,将甲乙两校这40份试卷的得分制作成如图所示的茎叶图,在这40份试卷中,从成绩在140分以上(含140分)的学生中任意抽取3人,这3人中数学成绩在全市排名前15名的人数记为![]() ,求随机变量
,求随机变量![]() 的分布列和期望.
的分布列和期望.
附:若![]() ,则
,则![]() ,
,![]() ,
,![]()
【答案】(1)180;(2)详见解析.
【解析】
(1)根据等距抽样的定义直接得到答案;
(2)根据正态分布得到全市排名前15名的成绩全部在146分以上,(含146分),根据茎叶图,得出![]() 的取值及其相应概率,即可得出随机变量
的取值及其相应概率,即可得出随机变量![]() 的分布列和期望.
的分布列和期望.
(1)因为200份试卷中用系统抽样中等距抽样的方法抽取了20份试卷,所以相邻两份试卷编号相差为1,所以试卷得分为144分的试卷编号180.
(2)∵![]() ,根据正态分布可知:
,根据正态分布可知: ![]() ,
,
∴![]() ,即全市排名前15名的成绩全部在146分以上,(含146分)
,即全市排名前15名的成绩全部在146分以上,(含146分)
根据茎叶图可知这40人中成绩在146分以上含146分的有3人,而成绩在140分以上含140分的有8人,
∴![]() 的取值为0,1,2,3
的取值为0,1,2,3
![]() ,
,![]()
![]() ,
,![]()
∴![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
因此![]() .
.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案【题目】自湖北武汉爆发新型冠状病毒肺炎疫情以来,各地医疗物资缺乏,各生产企业纷纷加班加点生产,某企业准备购买三台口罩生产设备,型号分别为A,B,C,已知这三台设备均使用同一种易耗品,提供设备的商家规定:可以在购买设备的同时购买该易耗品,每件易耗品的价格为100元;也可以在设备使用过程中,随时单独购买易耗品,每件易耗品的价格为200元.为了决策在购买设备时应同时购买的易耗品的件数,该单位调查了这三种型号的设备各60台,调查每台设备在一个月中使用的易耗品的件数,并得到统计表如下所示.
每台设备一个月中使用的易耗品的件数 | 6 | 7 | 8 | |
频数 | 型号A | 30 | 30 | 0 |
型号B | 20 | 30 | 10 | |
型号C | 0 | 45 | 15 | |
将调查的每种型号的设备的频率视为概率,各台设备在易耗品的使用上相互独立.
(1)求该单位一个月中A,B,C三台设备使用的易耗品总数超过21件(不包括21件)的概率;
(2)以该单位一个月购买易耗品所需总费用的期望值为决策依据,该单位在购买设备时应同时购买20件还是21件易耗品?