题目内容
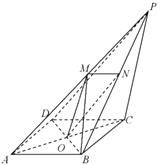
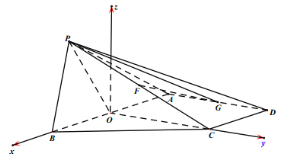
【题目】如图,四棱锥![]() 中,
中,![]() 是等边三角形,底面
是等边三角形,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.
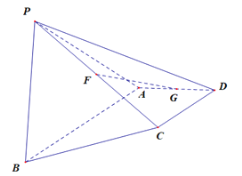
(1)①求证:![]() 平面
平面![]() ;
;
②求线段![]() 的长度;
的长度;
(2)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)①详见解析;②![]() ;(2)
;(2)![]() .
.
【解析】
(1)①通过证明面![]() 面
面![]() ,再利用面面平行的性质得证;②由余弦定理求解即可;
,再利用面面平行的性质得证;②由余弦定理求解即可;
(2)法一:作出图象,设![]() 到平面
到平面![]() 的距离设为
的距离设为![]() ,利用等体积法求出
,利用等体积法求出![]() ,进而可得直线
,进而可得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
法二:利用面面垂直的判定定理可证出平面![]() 平面
平面![]() ,建立空间直角坐标系,通过空间向量法,求出直线
,建立空间直角坐标系,通过空间向量法,求出直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
解:(1)①证明:取![]() 中点
中点![]() ,
,
则![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
②由①可知:
![]() ,
,![]() ,
,![]() ,
,
由余弦定理得到:
![]() .
.

(2)解法一:∵![]() ,
,![]() ,
,
∴![]() ,
,
又![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ,
,
延长![]() 到
到![]() ,使得
,使得![]() ,
,
则![]() 面
面![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 的中点,
的中点,![]() .
.
![]() 到平面
到平面![]() 的距离设为
的距离设为![]() ,
,
体积法求得:
![]() ,
,
∴![]() ,
,
∴![]() .
.
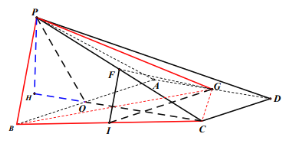
解法二:∵![]() ,
,![]() ,
,
∴![]() ,
,
又![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ,
,
以![]() 为坐标原点建立空间坐标系,得到
为坐标原点建立空间坐标系,得到
![]() ,
,![]() ,
,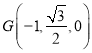 ,
,
延长![]() 到
到![]() ,使得
,使得![]() ,
,
则![]() 面
面![]() ,
,![]() ,
,
则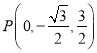 ,
,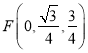 ,
,
∴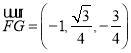 ,由于
,由于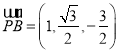 ,
,![]() ,
,
则法向量![]() ,
,
∴直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为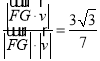 .
.

【题目】自湖北武汉爆发新型冠状病毒肺炎疫情以来,各地医疗物资缺乏,各生产企业纷纷加班加点生产,某企业准备购买三台口罩生产设备,型号分别为A,B,C,已知这三台设备均使用同一种易耗品,提供设备的商家规定:可以在购买设备的同时购买该易耗品,每件易耗品的价格为100元;也可以在设备使用过程中,随时单独购买易耗品,每件易耗品的价格为200元.为了决策在购买设备时应同时购买的易耗品的件数,该单位调查了这三种型号的设备各60台,调查每台设备在一个月中使用的易耗品的件数,并得到统计表如下所示.
每台设备一个月中使用的易耗品的件数 | 6 | 7 | 8 | |
频数 | 型号A | 30 | 30 | 0 |
型号B | 20 | 30 | 10 | |
型号C | 0 | 45 | 15 | |
将调查的每种型号的设备的频率视为概率,各台设备在易耗品的使用上相互独立.
(1)求该单位一个月中A,B,C三台设备使用的易耗品总数超过21件(不包括21件)的概率;
(2)以该单位一个月购买易耗品所需总费用的期望值为决策依据,该单位在购买设备时应同时购买20件还是21件易耗品?
【题目】某市对全市高二学生的期末数学测试成绩统计显示,全市10000名学生的数学成绩服从正态分布![]() .现从甲校高二年级数学成绩在100分以上(含100分)的共200份试卷中用系统抽样的方法抽取了20份试卷进行分析(试卷编号为001,002,…,200),成绩统计如下:
.现从甲校高二年级数学成绩在100分以上(含100分)的共200份试卷中用系统抽样的方法抽取了20份试卷进行分析(试卷编号为001,002,…,200),成绩统计如下:
试卷编号 |
|
|
|
|
|
|
|
|
|
|
试卷得分 | 109 | 118 | 112 | 114 | 126 | 128 | 127 | 124 | 126 | 120 |
试卷编号 |
|
|
|
|
|
|
|
|
|
|
试卷得分 | 135 | 138 | 135 | 137 | 135 | 139 | 142 | 144 | 148 | 150 |
注:表中试卷编![]() .
.
(1)写出表中试卷得分为144分的试卷编号(写出具体数据即可);
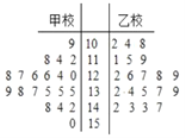
(2)该市又用系统抽样的方法从乙校中抽取了20份试卷,将甲乙两校这40份试卷的得分制作成如图所示的茎叶图,在这40份试卷中,从成绩在140分以上(含140分)的学生中任意抽取3人,这3人中数学成绩在全市排名前15名的人数记为![]() ,求随机变量
,求随机变量![]() 的分布列和期望.
的分布列和期望.
附:若![]() ,则
,则![]() ,
,![]() ,
,![]()
【题目】某动漫影视制作公司长期坚持文化自信,不断挖掘中华优秀传统文化中的动漫题材,创作出一批又一批的优秀动漫影视作品,获得市场和广大观众的一致好评,同时也为公司赢得丰厚的利润.该公司2013年至2019年的年利润![]() 关于年份代号
关于年份代号![]() 的统计数据如下表(已知该公司的年利润与年份代号线性相关):
的统计数据如下表(已知该公司的年利润与年份代号线性相关):
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
年利润 |
|
|
|
|
|
|
|
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程,并预测该公司2020年(年份代号记为
的线性回归方程,并预测该公司2020年(年份代号记为![]() )的年利润;
)的年利润;
(Ⅱ)当统计表中某年年利润的实际值大于由![]() 中线性回归方程计算出该年利润的估计值时,称该年为
中线性回归方程计算出该年利润的估计值时,称该年为![]() 级利润年,否则称为
级利润年,否则称为![]() 级利润年.将
级利润年.将![]() 中预测的该公司2020年的年利润视作该年利润的实际值,现从2015年至2020年这
中预测的该公司2020年的年利润视作该年利润的实际值,现从2015年至2020年这![]() 年中随机抽取
年中随机抽取![]() 年,求恰有
年,求恰有![]() 年为
年为![]() 级利润年的概率.
级利润年的概率.
参考公式: