Question

【题目】已知函数f1(x)＝x2，f2(x)＝alnx(其中a>0)．

(1)求函数f(x)＝f1(x)·f2(x)的极值；

(2)若函数g(x)＝f1(x)－f2(x)＋(a－1)x在区间(，e)内有两个零点，求正实数a的取值范围；

(3)求证：当x>0时，.(说明：e是自然对数的底数，e＝2.71828…)

Answer 1

【答案】(1) 函数f(x)的极小值为，无极大值．

(2) ．

(3)见解析.

【解析】分析：（1）求，求出方程的解，确定两侧的正负，得极值；

（2）求出，确定出在上递减，在上递增，结合零点存在定理可知在上有两个零点的条件，得出的范围；

（3）不等式可变形为，其中由（1）知的最小值为，下面只要求得的最大值，证明此最大值即可.

详解： (1)∵f(x)＝f1(x)·f2(x)＝ax2·lnx，

∴f ′(x)＝axlnx＋ax＝ax(2lnx＋1)(x>0，a>0)，

由f ′(x)>0，得x>e－，由f ′(x)<0，得0<x<e－，

故函数f(x)在(0，e－)上单调递减，在(e－，＋∞)上单调递增，

所以函数f(x)的极小值为f(e－)＝－，无极大值．

(2)函数g(x)＝x2－alnx＋(a－1)x，

则g′(x)＝x－＋(a－1)＝＝，

令g′(x)＝0，∵a>0，解得x＝1，或x＝－a(舍去)，

当0<x<1时，g′(x)<0，g(x)在(0,1)上单调递减；

当x>1时，g′(x)>0，g(x)在(1，＋∞)上单调递增．

函数g(x)在区间(，e)内有两个零点，

只需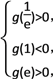即∴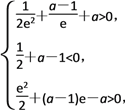

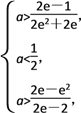
故实数a的取值范围是(，)．

(3)问题等价于x2lnx>－.由(1)知f(x)＝x2lnx的最小值为－.

设h(x)＝－，h′(x)＝－，

易知h(x)在(0,2)上单调递增，在(2，＋∞)上单调递减． 10分

∴h(x)max＝h(2)＝－，∵－－(－)＝－－＝＝>0，

∴f(x)min>h(x)max，∴x2lnx>－，故当x>0时，lnx＋－>0.