题目内容
如图,已知三棱锥 中,
中, ,
, ,
, 为
为 中点,
中点, 为
为 中点,且
中点,且 为正三角形。
为正三角形。

(Ⅰ)求证: //平面
//平面 ;
;
(Ⅱ)求证:平面 ⊥平面
⊥平面 ;
;
(III)若 ,
, ,求三棱锥
,求三棱锥 的体积.
的体积.
【答案】
(Ⅰ)、(Ⅱ)详见解析(III)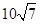 .
.
【解析】
试题分析:(Ⅰ)利用中位线性质得到线线平行,根据线面平行的判定判定直线与平面平行;(Ⅱ)利用正三角形中点得到线线垂直,根据平行推得线线垂直,利用直线与平面垂直判定面面垂直;(Ⅲ)利用三棱锥的体积公式计算体积.
试题解析:(Ⅰ)∵M为AB中点,D为PB中点,
∴MD//AP, 又∴MD 平面ABC
平面ABC
∴DM//平面APC. 3分
(Ⅱ)∵△PMB为正三角形,且D为PB中点.∴MD⊥PB.
又由(1)∴知MD//AP, ∴AP⊥PB.
又已知AP⊥PC ∴AP⊥平面PBC,
∴AP⊥BC, 又∵AC⊥BC. 7分
∴BC⊥平面APC, ∴平面ABC⊥平面PAC,
(Ⅲ)∵ AB=20
∴ MB=10 ∴PB=10
又 BC=4, .
.
∴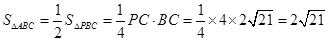 .
.
又MD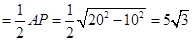 .
.
∴VD-BCM =
VM-BCD =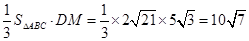 . 12分
. 12分
考点:直线与平面平行的判定;平面与平面垂直的判定,三棱锥体积计算.

练习册系列答案
相关题目

 中,
中, ,
, ,
, 为
为 中点,
中点, 为
为 中点,且
中点,且 为正三角形。
为正三角形。
 //平面
//平面 ;
; ⊥平面
⊥平面 ,
, ,求三棱锥
,求三棱锥 的体积.
的体积. 中,
中, ,
,
 ,
, 为
为 中点,
中点, 为
为 中点,且△
中点,且△ 为正三角形。
为正三角形。 ∥平面
∥平面 ;
;  ⊥平面
⊥平面
 中,
中, 面
面 ,
, ,
,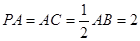 ,
, 为
为 上一点,
上一点, ,
, 分别为
分别为 的中点.
的中点.  .
. 与面
与面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值. (包括端点)上是否存在一点
(包括端点)上是否存在一点 ,使
,使 平面
平面