题目内容
已知椭圆C与椭圆C1:
+
=1有相同的焦点,且椭圆过点(2
,
),右焦点为F,
(1)求椭圆C的方程;
(2)若直线y=
x与椭圆C交于M、N两点,求△FMN的面积.
| x2 |
| 9 |
| y2 |
| 5 |
| 3 |
| 3 |
(1)求椭圆C的方程;
(2)若直线y=
| 1 |
| 2 |
分析:(1)依题意,可求椭圆C的焦点坐标(±2,0),方程为
+
=1,将点(2
,
)的坐标代入椭圆C的方程可求得a2,从而可得答案;
(2)由椭圆C的方程与直线y=
x联立,利用弦长公式可求得|MN|,由点到直线间的距离公式可求得点F到直线y=
x的距离d,从而可求△FMN的面积.
| x2 |
| a2 |
| y2 |
| a2-4 |
| 3 |
| 3 |
(2)由椭圆C的方程与直线y=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵椭圆C1:
+
=1的焦点坐标为(±2,0),
∴依题意设椭圆C的方程为
+
=1,将点(2
,
)的坐标代入椭圆C的方程,
得
+
=1,解得a2=16或a2=3(舍),
∴椭圆C的方程为:
+
=1.
(2)由
消去y得:x2=12,
∴x=±2
,y=±
.
不妨取M(2
,
),N(-2
,-
),
∴|MN|=
=
=
=2
.
又右焦点F(2,0)到直线y=
x即x-2y=0的距离d=
=
,
∴S△FMN=
|MN|•d=
×2
×
=2
.
| x2 |
| 9 |
| y2 |
| 5 |
∴依题意设椭圆C的方程为
| x2 |
| a2 |
| y2 |
| a2-4 |
| 3 |
| 3 |
得
(2
| ||
| a2 |
(
| ||
| a2-4 |
∴椭圆C的方程为:
| x2 |
| 16 |
| y2 |
| 12 |
(2)由
|
∴x=±2
| 3 |
| 3 |
不妨取M(2
| 3 |
| 3 |
| 3 |
| 3 |
∴|MN|=
[
|
| 12+48 |
| 60 |
| 15 |
又右焦点F(2,0)到直线y=
| 1 |
| 2 |
| 2 | ||
|
2
| ||
| 5 |
∴S△FMN=
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
2
| ||
| 5 |
| 3 |
点评:本题考查直线与圆锥曲线的关系,着重考查方程思想与韦达定理与弦长公式、三角形面积公式的综合应用,属于难题.

练习册系列答案
相关题目
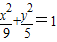 有相同的焦点,且椭圆过点
有相同的焦点,且椭圆过点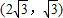 ,右焦点为F,
,右焦点为F,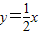 与椭圆C交于M、N两点,求△FMN的面积.
与椭圆C交于M、N两点,求△FMN的面积.