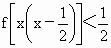题目内容
设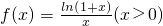
(Ⅰ)判断函数f(x)的单调性;
(Ⅱ)是否存在实数a,使得关于x的不等式ln(1+x)<ax在(0,+∞)上恒成立,若存在,求出a的取值范围,若不存在,试说明理由;
(Ⅲ)求证: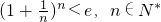 (其中e为自然对数的底数).
(其中e为自然对数的底数).
证明:(1)∵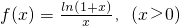
∴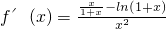 ,
,
设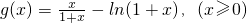 .
.
∴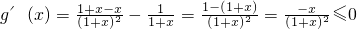 ,
,
∴y=g(x)在[0,+∞)上为减函数.
∴ ,
,
∴ ,
,
∴函数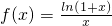 在(0,+∞)上为减函数.
在(0,+∞)上为减函数.
(2)ln(1+x)<ax在(0,+∞)上恒成立,?ln(1+x)-ax<0在(0,+∞)上恒成立,
设h(x)=ln(1+x)-ax,则h(0)=0,
∴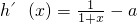 ,
,
若a≥1,则x∈[0,+∞)时,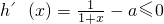 恒成立,
恒成立,
∴h(x)=ln(1+x)-ax在[0,+∞)上为减函数
∴ln(1+x)-ax<h(0)=0在(0,+∞)上恒成立,
∴ln(1+x)<ax在(0,+∞)上恒成立,
若a≤0显然不满足条件,
若0<a<1,则 时,
时, ,
,
∴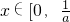 时h'(x)≥0,
时h'(x)≥0,
∴h(x)=ln(1+x)-ax在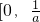 上为增函数,
上为增函数,
当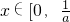 时,h(x)=ln(1+x)-ax>0,
时,h(x)=ln(1+x)-ax>0,
不能使ln(1+x)<ax在(0,+∞)上恒成立,
∴a≥1
(3)由(2)可知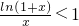 在(0,+∞)上恒成立,
在(0,+∞)上恒成立,
∴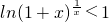 ,即
,即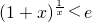 ,
,
取 ,即可证得
,即可证得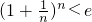 对一切正整数n成立.
对一切正整数n成立.
分析:(1)已知f(x),构造新的函数g(x),利用导数求函数单调的方法步骤;
(2)将ln(1+x)<ax在(0,+∞)上恒成立等价于ln(1+x)-ax<0在(0,+∞)上恒成立,构造新的函数h(x)=ln(1+x)-ax,x∈[0,+∞),依题意,我们所要求的a的取值范围,需要满足以下条件:能够使得h(x)在[0,+∞)上单调递减.
(3)由(2)可知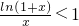 在(0,+∞)上恒成立,可以得到
在(0,+∞)上恒成立,可以得到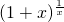 <e,只需令
<e,只需令 =n,即可.
=n,即可.
点评:本题综合性较强,主要考查利用导数研究函数的单调性,以此为主线,贯穿其中.但对以上三个问题的解答,关键是构造函数,这是函数这一章节的重点和难点.
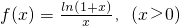
∴
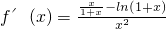 ,
,设
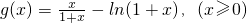 .
.∴
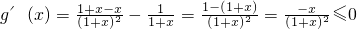 ,
,∴y=g(x)在[0,+∞)上为减函数.
∴
 ,
,∴
 ,
,∴函数
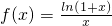 在(0,+∞)上为减函数.
在(0,+∞)上为减函数.(2)ln(1+x)<ax在(0,+∞)上恒成立,?ln(1+x)-ax<0在(0,+∞)上恒成立,
设h(x)=ln(1+x)-ax,则h(0)=0,
∴
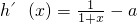 ,
,若a≥1,则x∈[0,+∞)时,
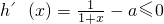 恒成立,
恒成立,∴h(x)=ln(1+x)-ax在[0,+∞)上为减函数
∴ln(1+x)-ax<h(0)=0在(0,+∞)上恒成立,
∴ln(1+x)<ax在(0,+∞)上恒成立,
若a≤0显然不满足条件,
若0<a<1,则
 时,
时, ,
,∴
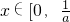 时h'(x)≥0,
时h'(x)≥0,∴h(x)=ln(1+x)-ax在
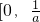 上为增函数,
上为增函数,当
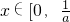 时,h(x)=ln(1+x)-ax>0,
时,h(x)=ln(1+x)-ax>0,不能使ln(1+x)<ax在(0,+∞)上恒成立,
∴a≥1
(3)由(2)可知
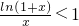 在(0,+∞)上恒成立,
在(0,+∞)上恒成立,∴
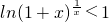 ,即
,即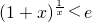 ,
,取
 ,即可证得
,即可证得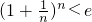 对一切正整数n成立.
对一切正整数n成立.分析:(1)已知f(x),构造新的函数g(x),利用导数求函数单调的方法步骤;
(2)将ln(1+x)<ax在(0,+∞)上恒成立等价于ln(1+x)-ax<0在(0,+∞)上恒成立,构造新的函数h(x)=ln(1+x)-ax,x∈[0,+∞),依题意,我们所要求的a的取值范围,需要满足以下条件:能够使得h(x)在[0,+∞)上单调递减.
(3)由(2)可知
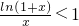 在(0,+∞)上恒成立,可以得到
在(0,+∞)上恒成立,可以得到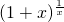 <e,只需令
<e,只需令 =n,即可.
=n,即可.点评:本题综合性较强,主要考查利用导数研究函数的单调性,以此为主线,贯穿其中.但对以上三个问题的解答,关键是构造函数,这是函数这一章节的重点和难点.

练习册系列答案
相关题目
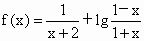 .
.
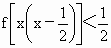
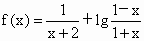 .
.