题目内容
已知点A、B是双曲线x2-=1上的两点,O为坐标原点,且满足 ·
· =0,则点O到直线AB的距离等于
=0,则点O到直线AB的距离等于
A. B. C.2 D.2
 ·
·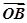 =0,则点O到直线AB的距离等于
=0,则点O到直线AB的距离等于A. B. C.2 D.2
A
分析:本题是关于圆锥曲线中的点到线的距离问题,由于双曲线为中心对称图形,为此可考查特殊情况,设A为y=x与双曲线在第一象限的交点,则得到B为直线y=-x与双曲线在第四象限的一个交点,因此直线AB与x轴垂直,点O到AB的距离就为点A或点B的横坐标的值,联立直线与双曲线的解析式,求出x的值即可.
解:由
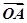 ·
·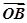 =0?OA⊥OB,由于双曲线为中心对称图形,
=0?OA⊥OB,由于双曲线为中心对称图形,令点A为直线y=x与双曲线在第一象限的交点,
因此点B为直线y=-x与双曲线在第四象限的一个交点,
因此直线AB与x轴垂直,点O到AB的距离就为点A或点B的横坐标的值,
由
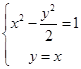 ,
,解得x=
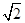 .
.故选A.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ABC的边AB,BC,CA的中点,O是△ABC的重心,则
ABC的边AB,BC,CA的中点,O是△ABC的重心,则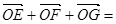 ( )
( )
 (B)
(B) 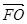 (C)
(C) 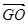 (D) 0
(D) 0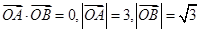 ,点
,点 在
在 内,且
内,且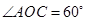 ,设
,设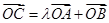 ,(
,(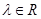 ) 则
) 则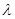 等于
等于 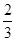
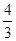
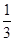
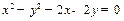 按向量
按向量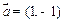 平移得到
平移得到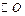 ,直线
,直线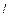 与
与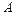 、
、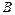 两点,若在
两点,若在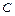 ,使
,使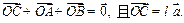 求直线
求直线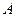 是单位圆与
是单位圆与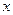 轴正半轴的交点,点
轴正半轴的交点,点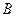 、
、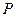 在单位圆上,且
在单位圆上,且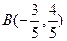 ,
,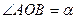 ,
,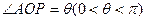 ,
,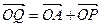 ,四边形
,四边形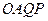 的面积为
的面积为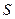 ,
,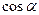 +
+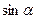
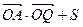 的最大值及此时
的最大值及此时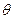 的值
的值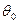 ;
;
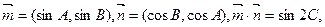 且A、B、C分别为△ABC的三边a、b、c所对的角.
且A、B、C分别为△ABC的三边a、b、c所对的角.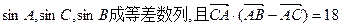 ,求c边的长.
,求c边的长.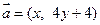 , 向量
, 向量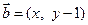 , 且
, 且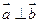 , 动点
, 动点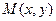 的轨迹为E.
的轨迹为E.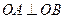 (O为坐标原点),并求出该圆的方程;
(O为坐标原点),并求出该圆的方程;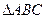 内部一点
内部一点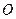 满足:
满足: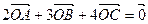 ,求:
,求: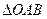 、
、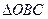 、
、 的面积的比.
的面积的比.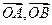 不共线(O为坐标原点),若
不共线(O为坐标原点),若 ,则C点所有可能的位置区域用阴影表示正确的是
,则C点所有可能的位置区域用阴影表示正确的是