题目内容
 与
与 是定义在R上的两个可导函数,若
是定义在R上的两个可导函数,若 ,
, 满足
满足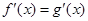 ,则
,则 与
与 满足
满足
A.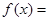  | B.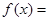 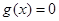 |
C.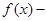  为常数函数 为常数函数 | D.  为常数函数 为常数函数 |
C
解析试题分析: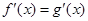 即
即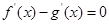 ,所以,
,所以,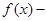
 为常数函数,故选C。
为常数函数,故选C。
考点:本题主要考查导数的计算,导数的运算法则。
点评:简单题,注意常数的导数为0.函数和差的导数等于函数导数的和差。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知曲线y= x2-2上一点P
x2-2上一点P ,则过点P的切线的方程是( )
,则过点P的切线的方程是( )
A.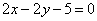 | B.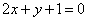 |
C.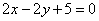 | D.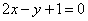 |
函数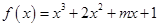 在区间
在区间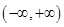 内单调递增,那么
内单调递增,那么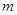 的范围为( )
的范围为( )
A.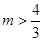 | B.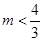 | C.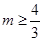 | D.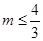 |
函数 的单调递增区间是
的单调递增区间是
A. | B.(0,3) | C.(1,4) | D. |
若曲线 在点
在点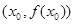 处的切线方程为
处的切线方程为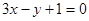 ,则( )
,则( )
A.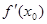 <0 <0 | B.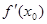 =0 =0 | C.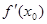 >0 >0 | D.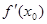 不存在 不存在 |
一个物体的运动方程为 ,其中
,其中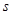 的单位是米,
的单位是米,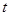 的单位是秒,那么物体在3秒末的瞬时速度是( )
的单位是秒,那么物体在3秒末的瞬时速度是( )
| A.3米/秒 | B.6米/秒 | C.5米/秒 | D.4米/秒 |
函数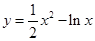 的单调递减区间为( )
的单调递减区间为( )
A. | B.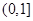 | C.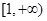 | D.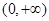 |
若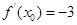 ,则
,则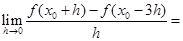
A.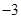 | B.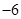 | C.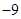 | D.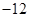 |
曲线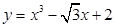 上的任意一点P处切线的斜率的取值范围是( )
上的任意一点P处切线的斜率的取值范围是( )
A.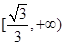 | B.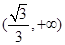 | C.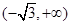 | D.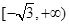 |