题目内容
函数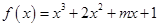 在区间
在区间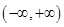 内单调递增,那么
内单调递增,那么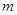 的范围为( )
的范围为( )
A.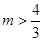 | B.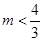 | C.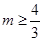 | D.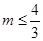 |
C
解析试题分析:因为函数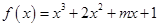 在区间
在区间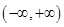 内单调递增,所以导函数
内单调递增,所以导函数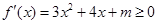 在
在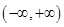 内恒成立,所以
内恒成立,所以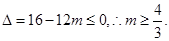
考点:本小题主要考查利用导数研究函数的单调性.
点评:导函数的正负决定原函数的增减,二次函数的恒成立问题可以借助图象,利用开口方向和判别式解决.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
一质点做直线运动,由始点经过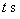 后的距离为
后的距离为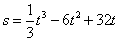 ,则速度为
,则速度为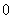 的时刻是( )
的时刻是( )
A.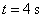 | B.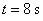 | C.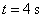 与 与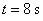 | D.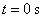 与 与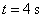 |
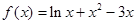 的极大值点是( )
的极大值点是( )
A.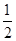 | B.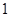 | C.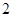 | D.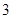 |
若定义在R上的函数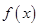 的导函数是
的导函数是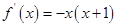 ,则函数
,则函数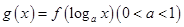 的单调递减区间是( )
的单调递减区间是( )
A.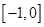 | B.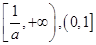 | C.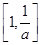 | D.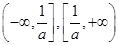 |
“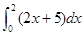 等于
等于
| A.9 | B.11 | C.14 | D.18 |
若函数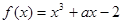 在区间
在区间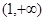 内是增函数,则实数
内是增函数,则实数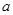 的取值范围是 ( )
的取值范围是 ( )
A.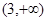 | B.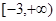 | C.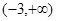 | D.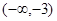 |
 与
与 是定义在R上的两个可导函数,若
是定义在R上的两个可导函数,若 ,
, 满足
满足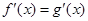 ,则
,则 与
与 满足
满足
A.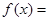  | B.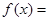 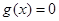 |
C.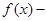  为常数函数 为常数函数 | D.  为常数函数 为常数函数 |
积分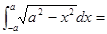 ( )
( )
A. | B.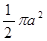 | C.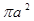 | D.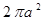 |
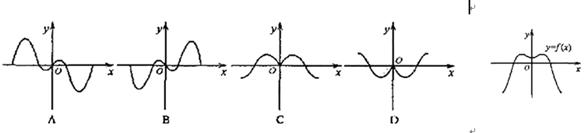
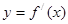 的图象可能是( )
的图象可能是( )