题目内容
自然数按照下表的规律排列,则上起第2013行,左起第2014列的数为( )
A.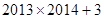 | B.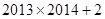 | C.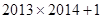 | D.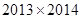 |
B
解析试题分析:先由表中的数据规律可知,第2013行中共有2013个,则上起第2013行,左起第2014列的数是在在第2014行第2014列的数的上面的一个数,结合等差数列的 通项可求解:表中的每行的第一个数构成的数列记为{an},则a2-a1=1,a3-a2=3,a4-a3=5…a2013-a2012=2×2012-1,以上式子叠加可得,a2013=2013×2011+2,由表中的数据规律可知,第2013行中共有2013个,∵第2014行的第一个数为2014×2012+2,∵第2014行的数是以2014×2012+2为首项,1为公差的等差数列,且横行有2014个数,,该数是2014×2012+2+2013,则上起第2013行,左起第2014列的数是在在第2014行第2014列的数的上面的一个数,即2014×2012+2+2013+1=2014×2012+2014+2=2014×2013+2,故选B
考点:数列的规律性
点评:本题是对数字变化规律的考查,观察数列的变化规律是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在数列{ }中,若
}中,若 ,则
,则 ( )
( )
| A.1 | B.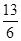 | C.2 | D.1.5 |
数列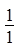 、
、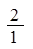 、
、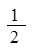 、
、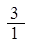 、
、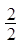 、
、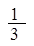 、
、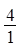 、
、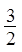 、
、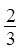 、
、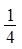 ……依次排列到第
……依次排列到第 项属于的范围是( )。
项属于的范围是( )。
A.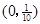 | B.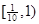 | C.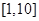 | D.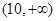 |
数列 中
中 ,则
,则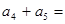 ( )
( )
| A.7 | B.8 | C.9 | D.10 |
已知数列的前几项为1,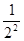 ,
,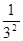 ,
, ,它的第n项(
,它的第n项(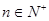 )是( )
)是( )
A.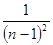 | B.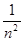 | C.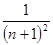 | D.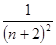 |
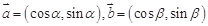 ,其中
,其中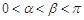 .
. 与
与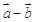 互相垂直;
互相垂直;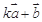 与
与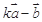 大小相等,求
大小相等,求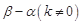 .
.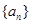 中,对任意正整数
中,对任意正整数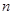 ,都有
,都有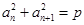 (常数),则称数列
(常数),则称数列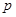 为“公方和”,若数列
为“公方和”,若数列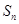 ,且“公方和”为
,且“公方和”为 ,首项
,首项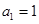 ,则
,则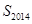 的最大值与最小值之和为( )
的最大值与最小值之和为( )
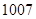

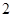

 }中,
}中,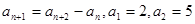 ,则
,则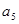 为___________.
为___________.