题目内容
若在数列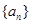 中,对任意正整数
中,对任意正整数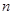 ,都有
,都有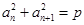 (常数),则称数列
(常数),则称数列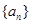 为“等方和数列”,称
为“等方和数列”,称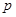 为“公方和”,若数列
为“公方和”,若数列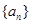 为“等方和数列”,其前
为“等方和数列”,其前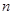 项和为
项和为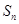 ,且“公方和”为
,且“公方和”为 ,首项
,首项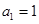 ,则
,则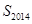 的最大值与最小值之和为( )
的最大值与最小值之和为( )
A. | B.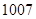 | C. | D.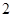 |

解析试题分析:由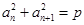 得
得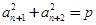 ,两等式相减得:
,两等式相减得: .又“公方和”为
.又“公方和”为 ,首项
,首项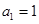 ,所以
,所以 .所以
.所以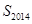 的最大值为1007,最小值为1005,其差为2.选D.
的最大值为1007,最小值为1005,其差为2.选D.
考点:1、新定义;2、数列.

练习册系列答案
相关题目
数列 的通项公式为
的通项公式为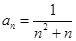 ,其前
,其前 项和为
项和为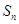 ,则
,则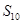 的值为 ( )
的值为 ( )
A.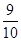 | B.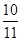 | C.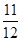 | D.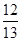 |
数列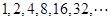 的一个通项公式是( )
的一个通项公式是( )
A.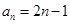 | B. | C.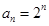 | D.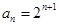 |
已知数列{an}的前n项和Sn=2n+1-2,等差数列{bn}中,b2=a2,且bn+3+bn-1=2bn+4,(n 2,n
2,n N+),则bn=
N+),则bn=
| A.2n+2 | B.2n | C.n-2 | D.2n-2 |
已知数列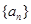 满足
满足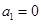 ,
,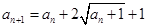 ,则
,则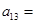 ( )
( )
| A.143 | B.156 | C.168 | D.195 |
两列数如下:7,10,13,16,19,22,25,28,31,......7,11,15,19,23,27,31,35,39,......第1个相同的数是7,第10个相同的数是( )
| A.115 | B.127 | C.139 | D.151 |
自然数按照下表的规律排列,则上起第2013行,左起第2014列的数为( )
A.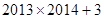 | B.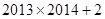 | C.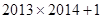 | D.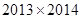 |
数列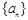 ,通项公式为
,通项公式为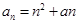 ,若此数列为递增数列,则
,若此数列为递增数列,则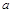 的取值范围是
的取值范围是
A.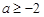 | B.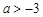 | C.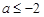 | D.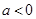 |
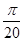 ,求证:a∥b.
,求证:a∥b.