题目内容
(本题满分14分)在数列 中,
中, ,
, ,
,
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 ;
;
(3)在(2)的条件下指出数列 的最小项的值,并证明你的结论。
的最小项的值,并证明你的结论。
 中,
中, ,
, ,
,(1)求数列
 的通项公式;
的通项公式;(2)求数列
 的前
的前 项和
项和 ;
;(3)在(2)的条件下指出数列
 的最小项的值,并证明你的结论。
的最小项的值,并证明你的结论。(1)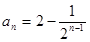 (
(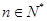 );
);
(2) =
=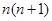
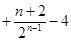 ;
;
(3)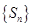 的最小项为
的最小项为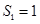
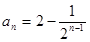 (
(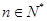 );
);(2)
 =
=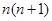
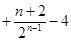 ;
;(3)
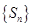 的最小项为
的最小项为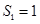
本试题主要是考查了数列中通项公式的求解,以及数列的求和的综合运用。
(1)因为由已知有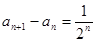
利用累差迭加即可求出数列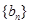 的通项公式
的通项公式
(2)结合第一问可知由(I)知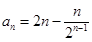 ,
,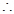
 =
=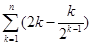
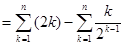 ,利用错位相减法得到。
,利用错位相减法得到。
(3)利用定义法得到数列的单调性,进而求解数列的最小项的求解的综合运用。
解:(1)由已知有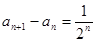
利用累差迭加即可求出数列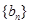 的通项公式:
的通项公式:
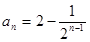 (
(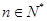 ) ------------------------ - 4分
) ------------------------ - 4分
2)由(I)知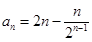 ,
,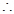
 =
=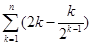
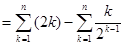
而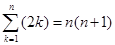 ,
,
对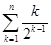 用错位相减法,易得
用错位相减法,易得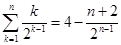
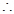
 =
=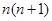
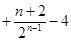 ----------------10分
----------------10分
(3)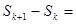
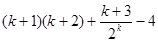 -
-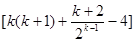
=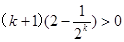
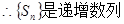
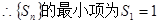 ----------------14分
----------------14分
(1)因为由已知有
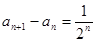
利用累差迭加即可求出数列
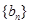 的通项公式
的通项公式(2)结合第一问可知由(I)知
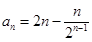 ,
,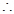
 =
=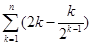
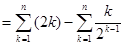 ,利用错位相减法得到。
,利用错位相减法得到。(3)利用定义法得到数列的单调性,进而求解数列的最小项的求解的综合运用。
解:(1)由已知有
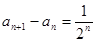
利用累差迭加即可求出数列
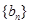 的通项公式:
的通项公式: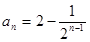 (
(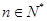 ) ------------------------ - 4分
) ------------------------ - 4分2)由(I)知
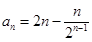 ,
,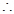
 =
=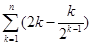
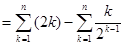
而
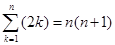 ,
,对
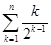 用错位相减法,易得
用错位相减法,易得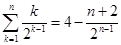
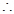
 =
=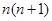
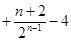 ----------------10分
----------------10分(3)
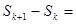
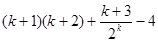 -
-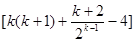
=
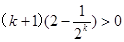
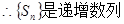
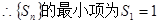 ----------------14分
----------------14分
练习册系列答案
相关题目
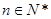 时,令
时,令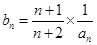 ,
,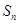 是数列{bn}的前n项和,求证:
是数列{bn}的前n项和,求证: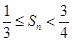
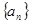 的通项公式为
的通项公式为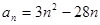 ,则数列
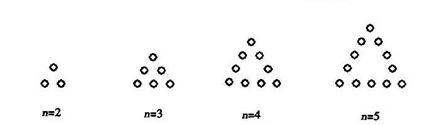
,则数列 个点,每个图形总的点数记为
个点,每个图形总的点数记为 ,则
,则 ( )
( )




 的前
的前 项和
项和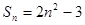 ,则
,则 .
.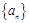 的前
的前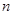 项和为
项和为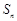 ,若
,若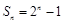 ,则
,则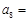
 满足
满足 则
则 的最小值为
的最小值为  中,
中, ,
, ,则
,则 的值是( )
的值是( )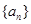 的前
的前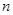 项和为
项和为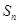 ,若点
,若点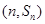 (
(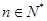 )在函数
)在函数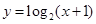 的反函数的图像上,则
的反函数的图像上,则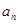 =________.
=________.