题目内容
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() (
(![]() ),设
),设![]() (
(![]() ),数列
),数列![]() 的前
的前![]() 项和
项和![]() .
.
(1)求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)利用“归纳—猜想—证明”求出![]() 的通项公式;
的通项公式;
(3)求数列![]() 的通项公式.
的通项公式.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() (
(![]() );(3)
);(3)![]() .
.
【解析】
(1)先代![]() ,求得
,求得![]() ,当
,当![]() 时,根据
时,根据![]() ,化简得到
,化简得到![]() 与
与![]() 的递推式,
的递推式,
再代![]() ,求得
,求得![]() ,并为求第(2)问提供基础;
,并为求第(2)问提供基础;
(2)由(1)归纳猜想![]() ,并用数学归纳法证明;
,并用数学归纳法证明;
(3)由(2)求得的![]() ,求出
,求出![]() ,并化简
,并化简![]() ,分析
,分析![]() ,发现可用裂项相消法求解,
,发现可用裂项相消法求解,
考虑消去方便,可对![]() 分奇数和偶数两种情况分析,最后合并得到答案.
分奇数和偶数两种情况分析,最后合并得到答案.
解:(1)由![]() ,令
,令![]() ,则
,则![]() ,得
,得![]() ,
,
当![]() 时,由
时,由![]() ,得
,得![]() ,得
,得![]() ,
,
令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() ,即
,即![]() ,
,![]() ,
,![]() .
.
(2)由(1)知![]() ,
,![]() ,
,![]() ,猜想
,猜想![]() ,
,
下面用数学归纳法证明:① 当![]() 时,由猜想知显然成立;
时,由猜想知显然成立;
②假设![]() 猜想成立,即
猜想成立,即![]() ,
,
则当![]() 时,由(1)有
时,由(1)有![]()
![]() ,
,
即当![]() 时,猜想
时,猜想![]() 也成立.
也成立.
综合①②可知,猜想![]() 成立,即
成立,即![]()
(3)由(2)知![]() ,当
,当![]() 时,
时,![]()
![]()
![]() ,
,
综合知:![]() ,又
,又![]() ,
,
则![]()
![]()
![]()
当![]() 为偶数时,
为偶数时,
![]()
![]()
![]()
![]()
![]()
当![]() 为奇数时,
为奇数时,![]()
![]()
![]()
![]()
![]()
![]()
![]()
综上可得![]()

 灵星计算小达人系列答案
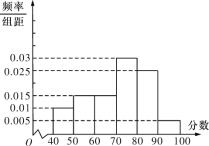
灵星计算小达人系列答案【题目】某班同学利用国庆节进行社会实践,对[25,55]岁的人群随机抽取![]() 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
组数 | 分组 | 低碳族的人数 | 占本组的频率 |
第一组 | [25,30) | 120 | 0.6 |
第二组 | [30,35) | 195 |
|
第三组 | [35,40) | 100 | 0.5 |
第四组 | [40,45) |
| 0.4 |
第五组 | [45,50) | 30 | 0.3 |
第六组 | [50,55] | 15 | 0.3 |
(1)补全频率分布直方图并求![]() 的值;
的值;
(2)从年龄段在[40,50)的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在[4,45)岁的概率.

【题目】高考复习经过二轮“见多识广”之后,为了研究考前“限时抢分”强化训练次数![]() 与答题正确率
与答题正确率![]() ﹪的关系,对某校高三某班学生进行了关注统计,得到如下数据:
﹪的关系,对某校高三某班学生进行了关注统计,得到如下数据:
| 1 | 2 | 3 | 4 |
| 20 | 30 | 50 | 60 |
(1)求![]() 关于
关于![]() 的线性回归方程,并预测答题正确率是100﹪的强化训练次数;
的线性回归方程,并预测答题正确率是100﹪的强化训练次数;
(2)若用![]() 表示统计数据的“强化均值”(精确到整数),若“强化均值”的标准差在区间
表示统计数据的“强化均值”(精确到整数),若“强化均值”的标准差在区间![]() 内,则强化训练有效,请问这个班的强化训练是否有效?
内,则强化训练有效,请问这个班的强化训练是否有效?
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
![]() =
= ,
, ![]() =
=![]() -
-![]()
![]() ,
,
样本数据![]() 的标准差为:
的标准差为: